The current in the series L-C-R circuit is
i=imsin(ωt+ϕ)
i=vm√R2+(Xc−XL)2sin(ωt+ϕ)
i=2imcos(ωt+ϕ)
Both (a) and (b)
The correct Answer is:D
To find the expression for the current in a series L-C-R circuit, we can follow these steps:
1. Understand the Circuit:
We have a series L-C-R circuit where an alternating current (AC) voltage V(t)=V0sin(ωt) is applied. The circuit consists of a resistor (R), an inductor (L), and a capacitor (C) connected in series.
2. Identify the Voltage Drops:
The voltage across each component can be expressed as:
- Voltage across the resistor: VR=I⋅R
- Voltage across the inductor: VL=I⋅jωL (where j is the imaginary unit)
- Voltage across the capacitor: VC=IjωC
3. Calculate the Impedance (Z):
The total impedance Z of the circuit can be calculated using the formula:
Z=√R2+(XL−XC)2
where XL=ωL (inductive reactance) and XC=1ωC (capacitive reactance). Therefore, the impedance becomes:
Z=√R2+(ωL−1ωC)2
4. Determine the Current:
The current I(t) in the circuit can be expressed as:
I(t)=Imsin(ωt+ϕ0)
where Im is the maximum current and ϕ0 is the phase angle. The maximum current can be calculated using Ohm's law for AC circuits:
Im=VmZ
where Vm is the peak voltage.
5. Express the Current:
Substituting for Im:
I(t)=VmZsin(ωt+ϕ0)
6. Phase Angle:
The phase angle ϕ0 depends on the relationship between the inductive and capacitive reactances:
tan(ϕ0)=XL−XCR
This indicates whether the circuit is inductive or capacitive.
Final Expression:
Thus, the expression for the current in the series L-C-R circuit is:
I(t)=VmZsin(ωt+ϕ0)
We have a series L-C-R circuit where an alternating current (AC) voltage V(t)=V0sin(ωt) is applied. The circuit consists of a resistor (R), an inductor (L), and a capacitor (C) connected in series.
The voltage across each component can be expressed as:
- Voltage across the resistor: VR=I⋅R
- Voltage across the inductor: VL=I⋅jωL (where j is the imaginary unit)
- Voltage across the capacitor: VC=IjωC
The total impedance Z of the circuit can be calculated using the formula:
Z=√R2+(XL−XC)2
where XL=ωL (inductive reactance) and XC=1ωC (capacitive reactance). Therefore, the impedance becomes:
Z=√R2+(ωL−1ωC)2
The current I(t) in the circuit can be expressed as:
I(t)=Imsin(ωt+ϕ0)
where Im is the maximum current and ϕ0 is the phase angle. The maximum current can be calculated using Ohm's law for AC circuits:
Im=VmZ
where Vm is the peak voltage.
Substituting for Im:
I(t)=VmZsin(ωt+ϕ0)
The phase angle ϕ0 depends on the relationship between the inductive and capacitive reactances:
tan(ϕ0)=XL−XCR
This indicates whether the circuit is inductive or capacitive.
Thus, the expression for the current in the series L-C-R circuit is:
I(t)=VmZsin(ωt+ϕ0)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROMAGNETIC INDUCTIONExercise:Example 2
Explore 28 Videos
- ELECTROMAGNETIC INDUCTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROMAGNETIC INDUCTIONExercise:Example 30
Explore 1 Video
- ELECTROMAGNETIC INDUCTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROMAGNETIC INDUCTIONExercise:MHT CET CONER
Explore 34 Videos
- ELASTICITY Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELASTICITY Exercise:MHT CET CORNER
Explore 16 Videos
- ELECTRONS AND PROTONSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTRONS AND PROTONSExercise:MHT CET CORNER
Explore 19 Videos
Similar Questions
Knowledge Check
The phase difference between voltage and current in series L-C circuit is
A0∘BπCπ2Dπ3Assertion: In series L−R circuit voltage leads the current.
Reason: In series L−C circuit leads the voltage.AIf both the assertion and reason are true and reason is a true explantion of the assertion.BIf both the assertion and reason are true but the reason is not true the correct explantion of the assertion.CIf the assertion is true but reason falseDIf both the assertion and reason are false.The value of current at resonance in a series L-C-R circuit is affected by the value of
AR onlyBC onlyCL onlyDL, C and R
When current (I) in R-L series circuit is constant where L is a pure inductor, The following statements are given
View SolutionAt resonance the peak value of current in L−C−R series circuit is
View SolutionIn terms of q, the voltage equation for series L-C-R circuit is given by
View SolutionIn the given figure , a series L-C-R circuit is connected to a variable frequency source of 230 V . The impedance and amplitude of the current at the resonating frequency will be
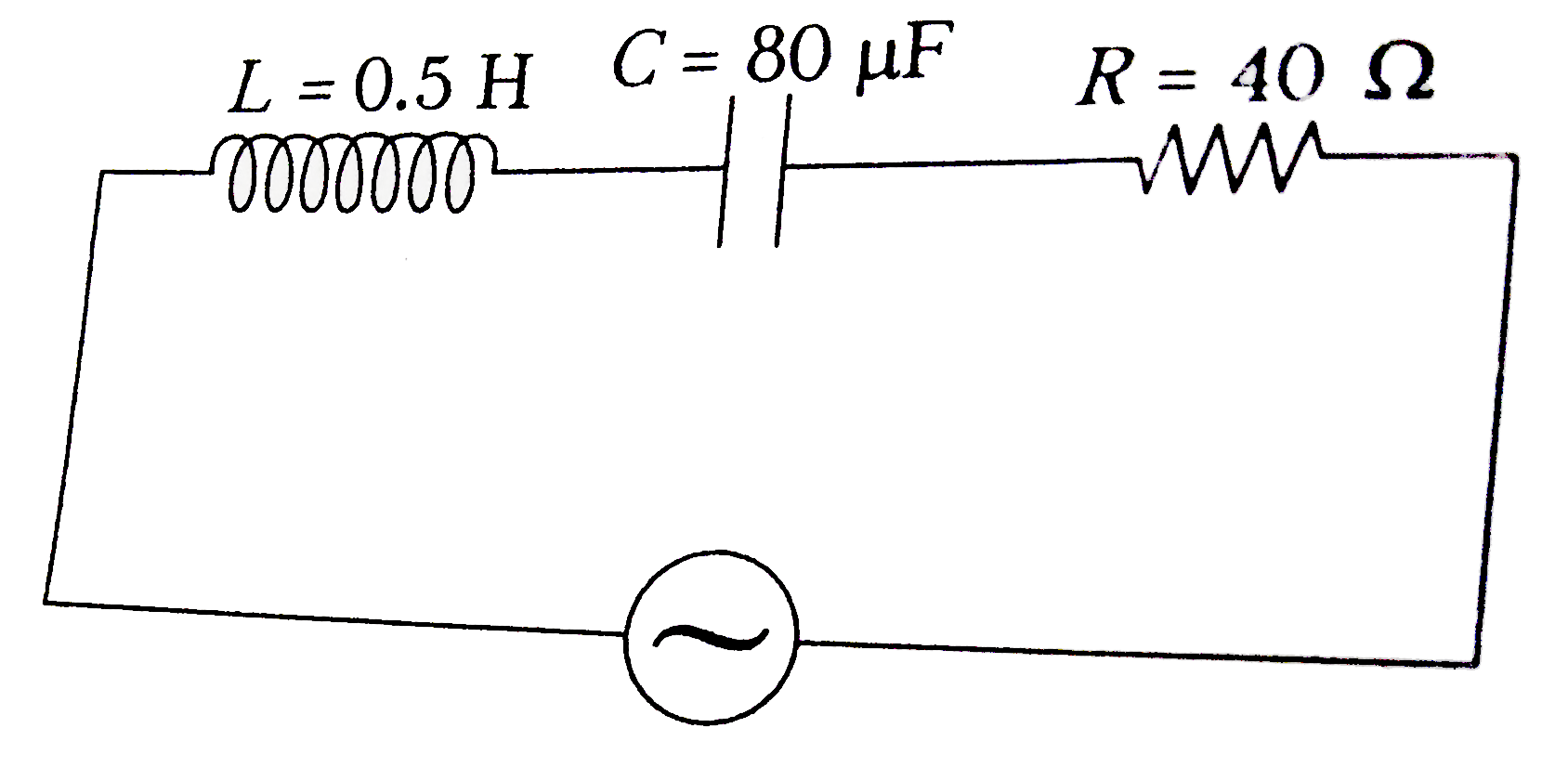
View SolutionIn L−C−R series AC circuit,
View Solution

