Three rods A,B and C have the same dimensions Their conductivities are KA K and KC respectively A and B are placed end to end with their free ends kept at certain temperature difference C is placed separately with its ends kept at same temperature difference The two arrangements conduct heat at the same rate Kc must be equal to .
KA+KB
KA+KBKAKB
12(KA+KB)
KA+KBKAKB
The correct Answer is:D
To solve the problem, we need to find the thermal conductivity KC of rod C such that the heat conduction rates through the two arrangements (rods A and B in series, and rod C separately) are the same.
1. Understanding the Setup:
- Rods A and B are placed end to end, and both have the same dimensions. Their thermal conductivities are KA and KB.
- Rod C is placed separately with the same temperature difference across its ends.
2. Thermal Resistance of Rods A and B in Series:
- The total thermal resistance RAB of rods A and B in series can be expressed as:
RAB=RA+RB
- The thermal resistance R of a rod is given by:
R=LK⋅A
where L is the length, K is the thermal conductivity, and A is the cross-sectional area.
- Therefore, for rods A and B:
RA=LKA⋅AandRB=LKB⋅A
- Thus, the total resistance becomes:
RAB=LKA⋅A+LKB⋅A=LA(1KA+1KB)
3. Thermal Resistance of Rod C:
- The thermal resistance RC of rod C is given by:
RC=LKC⋅A
4. Setting the Resistances Equal:
- For the heat conduction rates to be the same, the thermal resistances must be equal:
RAB=RC
- Substituting the expressions for RAB and RC:
LA(1KA+1KB)=LKC⋅A
5. Simplifying the Equation:
- Canceling LA from both sides (assuming L and A are not zero):
1KA+1KB=1KC
6. Finding KC:
- Rearranging the equation gives:
1KC=1KA+1KB
- Taking the reciprocal:
KC=KA⋅KBKA+KB
Final Answer:
KC=KA⋅KBKA+KB
- Rods A and B are placed end to end, and both have the same dimensions. Their thermal conductivities are KA and KB.
- Rod C is placed separately with the same temperature difference across its ends.
- The total thermal resistance RAB of rods A and B in series can be expressed as:
RAB=RA+RB
- The thermal resistance R of a rod is given by:
R=LK⋅A
where L is the length, K is the thermal conductivity, and A is the cross-sectional area.
- Therefore, for rods A and B:
RA=LKA⋅AandRB=LKB⋅A
- Thus, the total resistance becomes:
RAB=LKA⋅A+LKB⋅A=LA(1KA+1KB)
- The thermal resistance RC of rod C is given by:
RC=LKC⋅A
- For the heat conduction rates to be the same, the thermal resistances must be equal:
RAB=RC
- Substituting the expressions for RAB and RC:
LA(1KA+1KB)=LKC⋅A
- Canceling LA from both sides (assuming L and A are not zero):
1KA+1KB=1KC
- Rearranging the equation gives:
1KC=1KA+1KB
- Taking the reciprocal:
KC=KA⋅KBKA+KB
KC=KA⋅KBKA+KB
Topper's Solved these Questions
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-III (C.W)
Explore 1 Video
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL- (C.W)
Explore 25 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL - 2 (C.W)
Explore 1 Video
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:STATEMENT TYPE QUESTION
Explore 23 Videos
Similar Questions
Three rods of the same dimension have thermal conductivities 3K, 2K and K. They are arranged as shown in fig. Given below, with their ends at 100∘C,50∘C and 20∘C. The temperature of their junction is :-

View SolutionThree rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below

Then , the temperature of the junction in steady - state is
View Solution
Knowledge Check
As the temperature difference between the ends of a conductor increase the heat transfer rate by conduction____
AincreasesBdecreasesCremains sameDNone of theseAs the temperature difference between the ends of a conductor increase the heat transfer rate by conduction____
AincreasesBdecreasesCremains sameDNone of theseThe three rods described in the previous question are placed individually, with their ends kept at the same temperature difference. The rate of heat flow through C is equal to the rate of combined heat flow through A and B. kc must be equal to
AkA+kBBkAkBkA+kBC12(kA+kB)D2(kAkBkA+kB)
Three rods of same dimensions have thermal conductivities 3K, 2k and K, with their ends at 100∘C,50∘Cand0∘C respectively . They re arranged as shown in the diagram . The temperature of the junction J in steady -state is
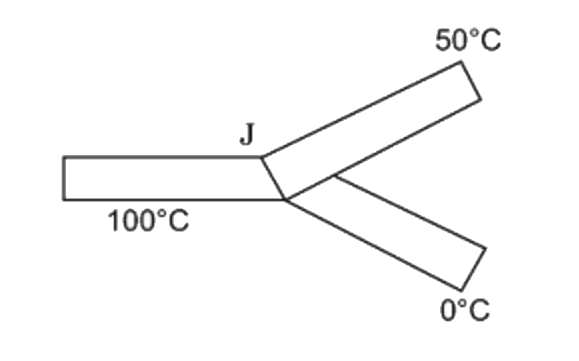
View SolutionThree rods of the same dimensions have thermal conductivities 3k , 2k and k . They are arranged as shown, with their ends at 100∘C,50∘C and 0∘C. The temperature of their junction is :-
_E01_022_Q01.png)
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionRate of heat flow through two conducting rods of identiclal dimensions having thermal conductivities K1 and K2 and Q1 and Q2 when their ends are maintained at the same difference of temperature individually. When the two rods are joined in series with their ends maintained at the same temperature difference (as shown in the figure), the rate of heat flow will be

View SolutionThree rods of same dimensions have thermal condutivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .
.
View Solution

