Two soap bubble of radii r1 and r2 combime to form a single bubble of radius r under isothermal conditions . If the external pressure is P, prove that surface tension of soap solution is given by S=P(r3−r31−r32)4(r21+r22−r2).
P0(R3+R31+R32)4(R2+R21+R22)
P0(R31+R32−R3)4(R2−R21−R22)
P0(R31+R32−R3)
4P0(R31+R32−R3)
According to isothermal process, PV=P1V1+P2V2
(P0+4TR)43πR3=(P0+4TR1)43πR31+(P0+4TR2)43πR32
P0(R3−R31−R32)=4T(R21+R22−R2)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Illustration
Explore 62 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EVALUATE YOURSELF - 1
Explore 2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 1 (H.W)
Explore 55 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
A soap bubble of radius r si blown up to form of bubble of radius 3r under isothermal conditions . What is the energy spent in doing so if the surface tension of soap solution is S.
View SolutionTwo soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View Solution
Knowledge Check
A soap bubble of radius 'r' is blown up to form a bubble of radius 2r under isothemal conditions. If σ be the surface tension of soap solution , the energy spent in doing so is
A3πσr2B6πσr2C12πσr2D24πσr2Two spherical soap bubbles of radii r1 and r2 in vacuume collapse under isothermal condition. The resulting bubble has radius R such that
AR=r1+r2BR=(r1+r2)12CR=√r21+r22DR=[(r2r2(r1+r2)]Two soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
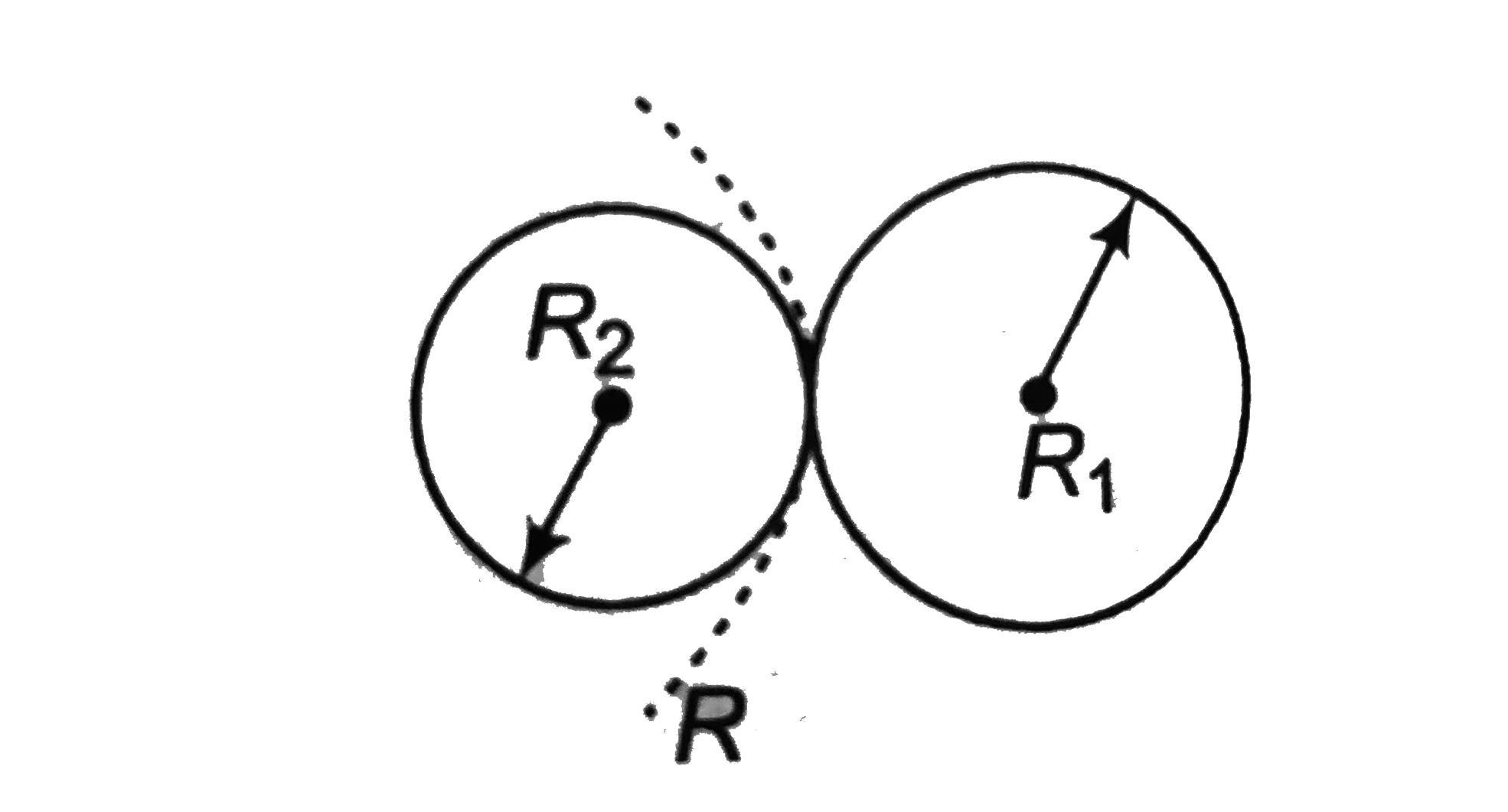 .AR=R1−R2BR=R1−R22C1R=1R2−1R1D1R=1R2+1R1
.AR=R1−R2BR=R1−R22C1R=1R2−1R1D1R=1R2+1R1
Under isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View SolutionTwo soap bubbles of radius R1 and R2 combine isothermally to form a new soap bubble. Find radius of new soap bubble
View SolutionTwo soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
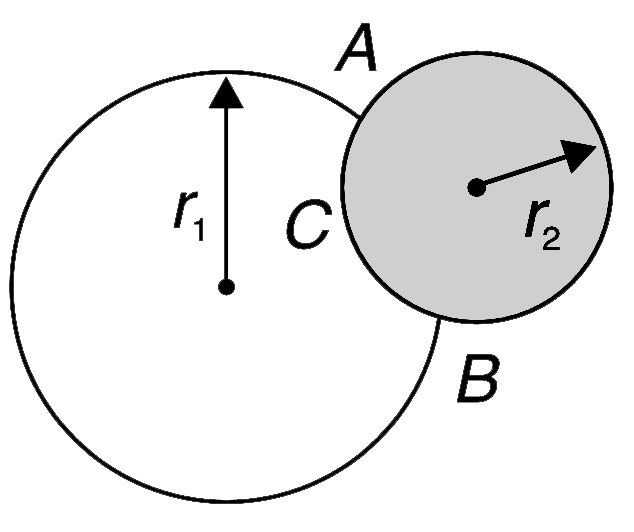
View SolutionTwo soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionA soap bubble of radius R has formed at normal temperature and pressure under isothermal conditions. Complete the work done. The surface tension of soap solution is T.
View Solution

