Water flows through a non-uniform tube of area of cross section A, B and C whose values are 25, 15 and 35cm2 resprectively. The ratio of the velocities of water at the sections A,B and C is
5:3:7
7:3:5
21:35:15
1:1:1
The correct Answer is:C
To find the ratio of the velocities of water at sections A, B, and C in a non-uniform tube, we can use the principle of conservation of mass, which states that the mass flow rate must remain constant throughout the tube. This means that the product of the cross-sectional area (A) and the velocity (V) at any point in the tube is constant.
1. Identify the Areas:
- Area at section A, AA=25cm2
- Area at section B, AB=15cm2
- Area at section C, AC=35cm2
2. Apply the Continuity Equation:
The continuity equation states that:
AA⋅VA=AB⋅VB=AC⋅VC
where VA,VB, and VC are the velocities at sections A, B, and C, respectively.
3. Set Up the Equations:
From the continuity equation, we can write:
25⋅VA=15⋅VB=35⋅VC
4. Express Velocities in Terms of Each Other:
We can express the velocities in terms of a common variable:
VA=1525VBandVA=3525VC
Simplifying these gives:
VA=35VBandVA=75VC
5. Find Ratios:
Now we can find the ratios of the velocities:
- From VA=35VB, we can express VB in terms of VA:
VB=53VA
- From VA=75VC, we can express VC in terms of VA:
VC=57VA
6. Combine the Ratios:
Now we can write the ratios of the velocities:
VA:VB:VC=VA:53VA:57VA
This simplifies to:
1:53:57
7. Clear the Fractions:
To eliminate the fractions, we can multiply through by the least common multiple of the denominators (3 and 7):
1⋅21:53⋅21:57⋅21=21:35:15
8. Final Ratio:
Thus, the final ratio of the velocities is:
VA:VB:VC=21:35:15
Final Answer:
The ratio of the velocities of water at sections A, B, and C is 21:35:15.
- Area at section A, AA=25cm2
- Area at section B, AB=15cm2
- Area at section C, AC=35cm2
The continuity equation states that:
AA⋅VA=AB⋅VB=AC⋅VC
where VA,VB, and VC are the velocities at sections A, B, and C, respectively.
From the continuity equation, we can write:
25⋅VA=15⋅VB=35⋅VC
We can express the velocities in terms of a common variable:
VA=1525VBandVA=3525VC
Simplifying these gives:
VA=35VBandVA=75VC
Now we can find the ratios of the velocities:
- From VA=35VB, we can express VB in terms of VA:
VB=53VA
- From VA=75VC, we can express VC in terms of VA:
VC=57VA
Now we can write the ratios of the velocities:
VA:VB:VC=VA:53VA:57VA
This simplifies to:
1:53:57
To eliminate the fractions, we can multiply through by the least common multiple of the denominators (3 and 7):
1⋅21:53⋅21:57⋅21=21:35:15
Thus, the final ratio of the velocities is:
VA:VB:VC=21:35:15
The ratio of the velocities of water at sections A, B, and C is 21:35:15.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 2 (C.W)
Explore 40 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 3
Explore 29 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:C.U.Q
Explore 117 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
Water flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through the tubes shown in figure. The areas of cross-section of the wide and the narrow portions of the tube are 5cm2 and 2cm2 respectively. The rate of flow of water through the tube is 500cm3/s. Find the difference of mercury levels in the U-tube.
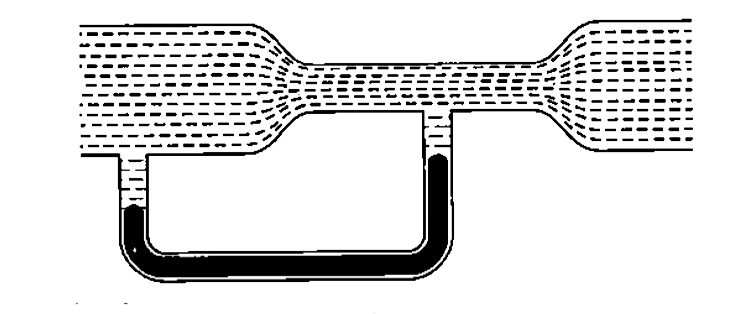
View Solution
Knowledge Check
Water flows through a vertical tube of varible cross-section. The area of cross-section at A and B 6 and 3 mm2 respectively. If 12c c of water enters per second through A, find the pressure difference PA−PB.(g=10m/s2). The separation between the cross-section at A and B is 100 cm.
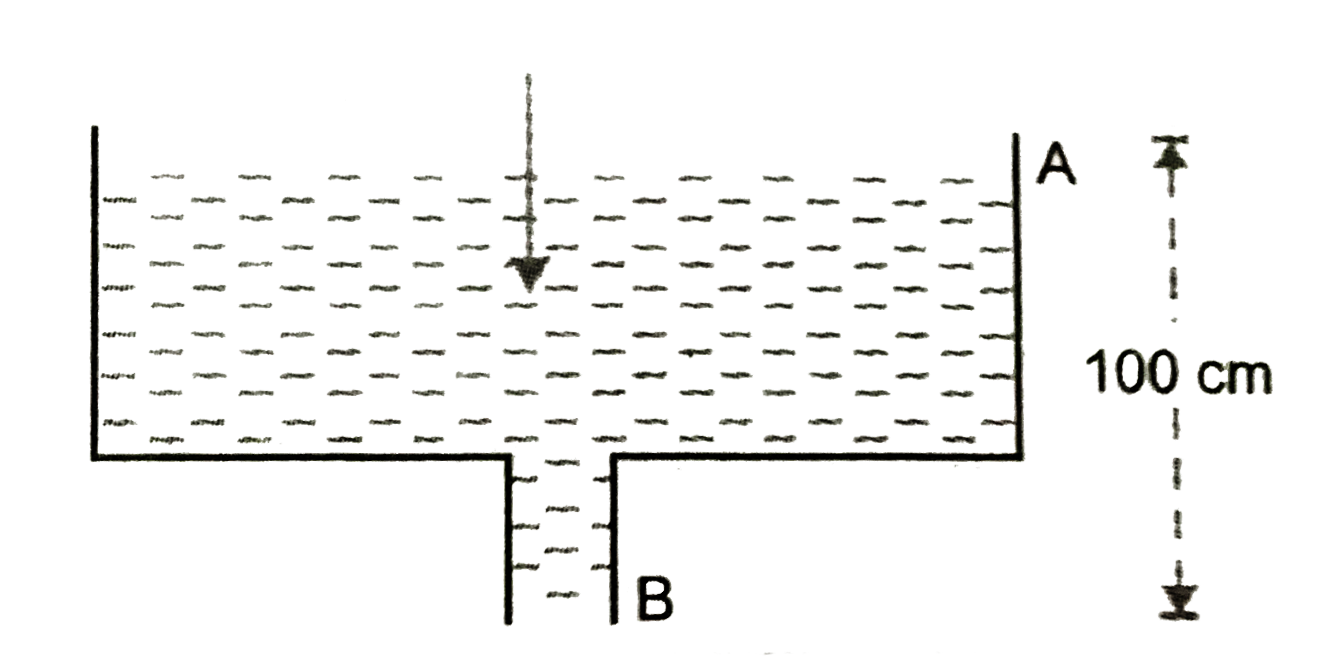 A1.6×105dyne/cm2B2.29×105dyne/cm2C5.9×105dyne/cm2D3.9×105dyne/cm2
A1.6×105dyne/cm2B2.29×105dyne/cm2C5.9×105dyne/cm2D3.9×105dyne/cm2An ideal fluid flows through a pipe of circular cross section made of two sections with diameters 2.5 cm and 3.75 cm. The ratio of the velocities in the two pipes is
A9:4,B3:2,C√3:√2D√2:√3water is flowing through a tube of non-uniform cross-section. If the radii of the tube at the ebtrance and the exit are in the ratio 3:2 then the ratio of the velocites of flow of watern at the entrance and the exit is
A9:4B4:9C8:27D27:8
Water flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5m. If the speed of water at A is 10 cms−1 find a the speed at B and b the difference in pressures at A and B.

View SolutionWaster flows throgh a horizontal tube of variable cross section.The area of cross section at A and B are 4 mm2and2mm2 respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference PA−PB.

View SolutionWater flows through a horizontal pipe of varying area of cross-section at the rate 5 cubic metre per minute. What is the velocity of water at a point where pipe radius is 10 cm?
View SolutionWater flows through a horizontal tube as shown in figure. If the difference of heights of water colun in the vertical tubes is 2 cm and the area of cross section at A and B are 4cm2and2cm2 respectively, find the rate of flow of water across any section.

View SolutionAn ideal fluid flows through a pipe of circular cross section made of two section with diamters 2.5 cm and 9.76 cm. The ratio of the velocities in the two pipes is
View Solution

