A steel of area of cross-section A and length 2L is calmped family between two rigid supports separated by a distance '2L'. A body is hung from the middle point sags by a distance x. Calculate the mass of the body body and the angle made by the string with the horizontal. (Young's modulus of Steel =Y)
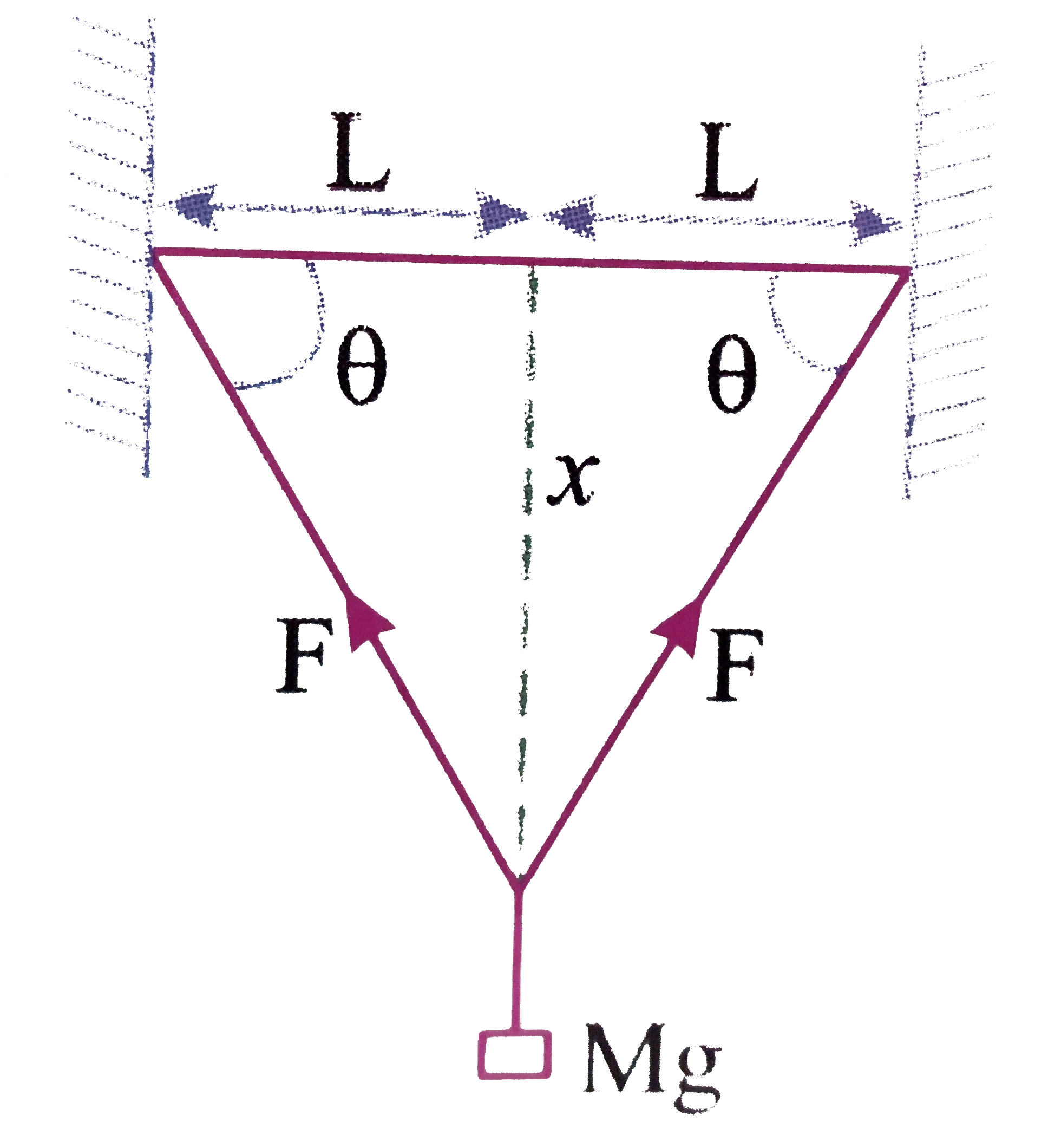
Since θ is small, sinθ≈tanθ=xL
Y=FALe,F=YAL[(L2+x2)1/2−L]
=YAL[L(1+x22L2)−L]=YAL[L+x22L−L]
F=Yax22L2.....(1) From the fig.
2Fsinθ=Mg,2Fθ=Mg, from (1)
2(YAx22L2)θ=Mg⇒YAx2L2×xL=Mg⇒M=YAx3L3g
x3L3=MgYA⇒xL=(MgYA)1/3, Since, Tanθ=xL
Tanθ=(MgYA)1/3⇒θ=Tan−1(MGYA)1/3
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - C.U.Q
74 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-I (C.W)
37 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - III
30 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)
31 Videos
Similar Questions
A sonometer wire of density ρ and radius r is held between two bridges at a distance L apart . Tension in the wire is T. then the fundamental frequency of the wire will be
View SolutionA steel wire of length 3.0m is stretched through 3.0 mm. the cross-sectional area of the wire is 5.0mm2. Calculate the elastic potential energy stroed in the wire in the stretched condition. Young's modulus of steel is 2.0×1011Nm−2.
View Solution
Knowledge Check
The force of gravitation between two bodies of mass 2 kg each separated by a distance of 2 m in vacuum is
A6.67×10−11NB6.67×10−10NC6.67×10−9NDnone of theseA metal bar of length L and area of cross-section A is clamped between two rigid supports. For the material of the rod. It Young's modulus is T and Coefficient if linear expansion is α. If the temperature of the rod is increased by Δt∘C, the force exerted by the rod on the supports is
AYALΔtBYAαΔtCYLαΔtADYαALΔtA steel wire of negligible mass, length 2I, cross sectional area 'A' and Young's modulus 'Y' is held between two rigid walls. A small body of mass 'm' is suspended from its middle point 'O' as shown. The vertical descent of the middle point 'O' of the wire is
 Al(mgAY)1/3Bl(2mgAY)1/3Cl(4mgAY)1/3Dl(6mgAY)1/3
Al(mgAY)1/3Bl(2mgAY)1/3Cl(4mgAY)1/3Dl(6mgAY)1/3
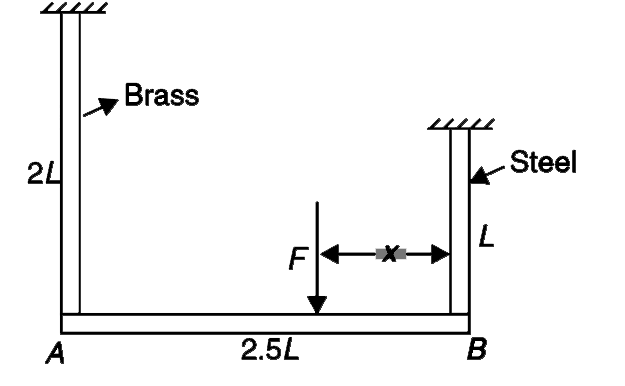
A very stiff bar (AB) of negligible mass is suspended horizontally by two vertical rods as shown in figure. Length of the bar is 2.5 L. The steel rod has length L and cross sectional radius of r and the brass rod has length 2L and cross sectional radius of 2r . A vertically downward force F is applied to the bar at a distance x from the steel rod and the bar remains horizontal. Find the value of x if it is given that ratio of Young’s modulus of steel and brass is YsYB=2.
View SolutionA brass wire of cross-sectional area 2mm2 is suspended from a rigid support and a body of volume 100cm2 is attached to its other end. If the decrases in the length of the wire is 0.11mm, when the body is completely immersed in water, find the natural length of the wire.
View SolutionA cord of mass m length L, area of cross section A and Young's modulus y is hanging from a ceiling with the help of a rigid support. The elogation developed in the wire due to its own weight is
View SolutionA mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
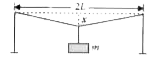
A mass m is suspended from the midpoint of the wire. Strain in the wire is
View SolutionA mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
View Solution