(n−1) equal point masses each of mass m are placed at the vertices of a angular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
b=−an−1
b=−a2n−1
b=−a(n−1)2
b=−3a2n−1
The correct Answer is:A
Let b be the position vector of the centre of mass of a regular n-polygon
(n−1) equal point masses are placed at
(n−1) vertices of the regular n-polygon
therefore, for its centre of mass
tCM=(n−1)mb+man−1m+n=0 ( ∴ centre of mass lies at centre)
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -I(H.W)
Explore 58 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-III
Explore 66 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
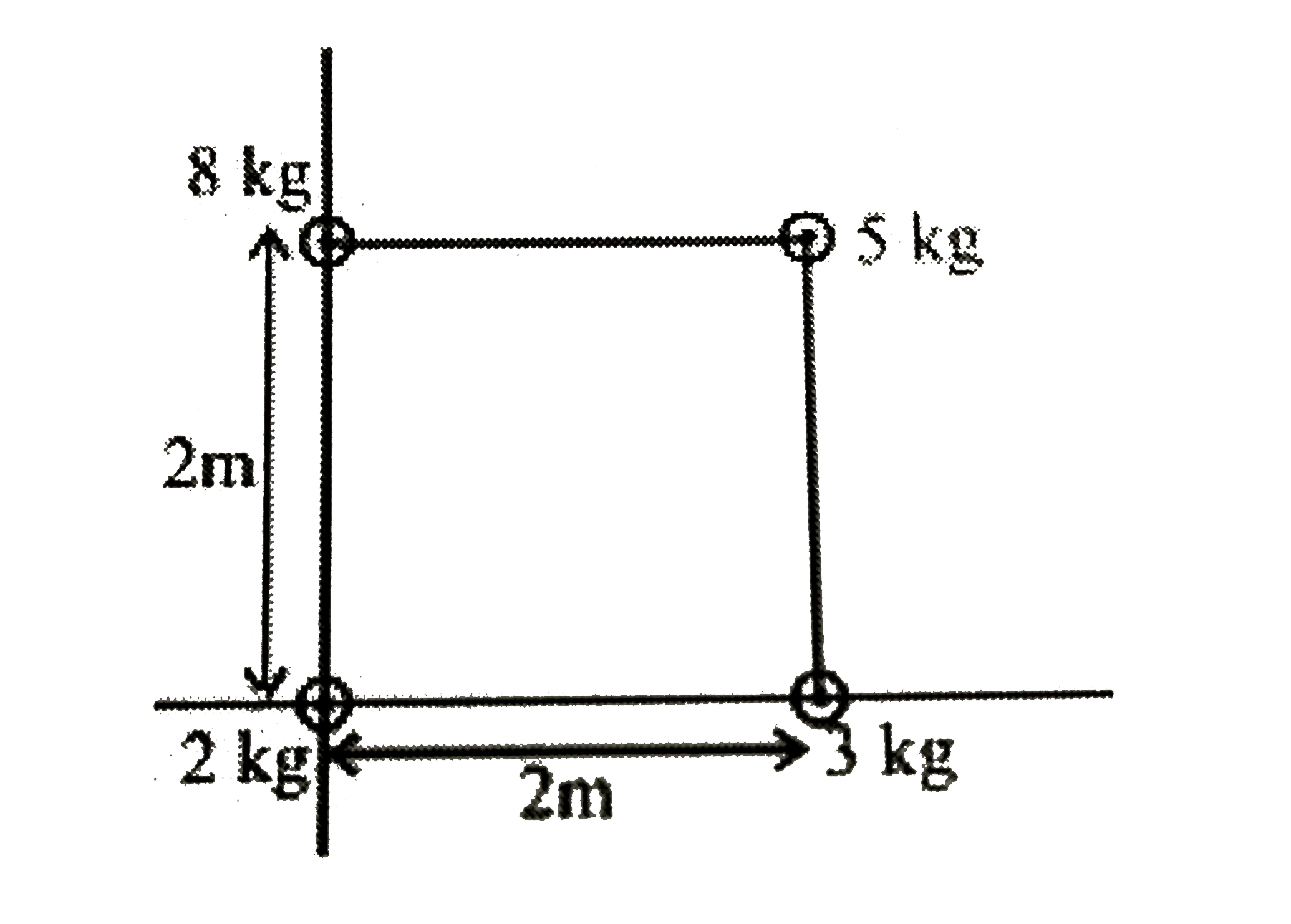
Position of the centre of mass is :-
View SolutionThree identical spheres , each of mass M , are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 2 m . Taking their point of intersection as the origin , find the position vector of centre of mass
View Solution
Knowledge Check
Three identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
A√3(ˆi−ˆj)Bˆi√3+ˆjCˆi+ˆj/3Dˆi+ˆj/√3Three particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and ˆi,ˆj,ˆk are unit vectors)
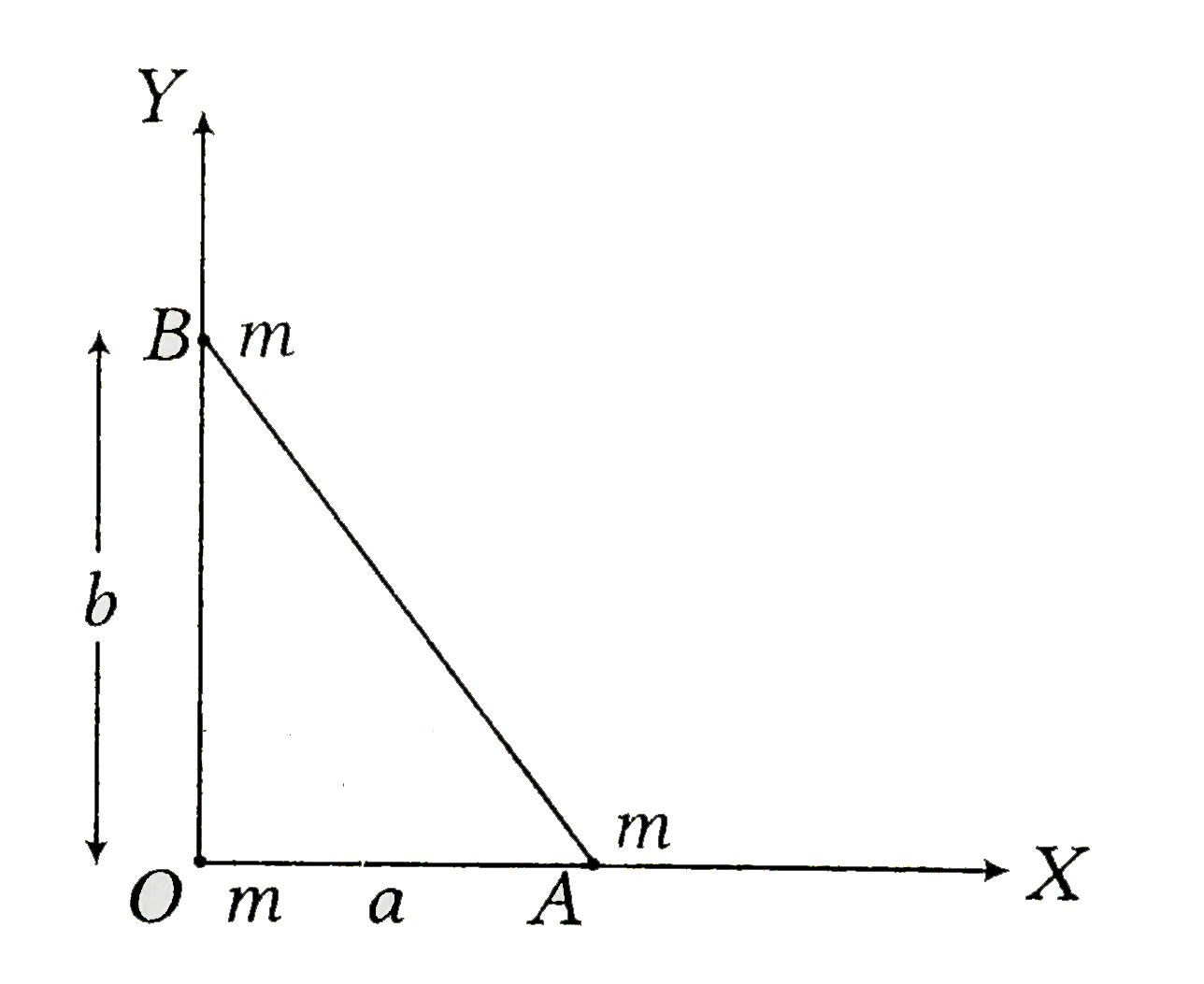 A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)
A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3
If a charge q is placed at each vertex of a regular polygon, the net electric field at its centre is zero. Show it.
View Solution(i) A regular polygon has 2016 sides and r is the radius of the circle circumscribing the polygon. Particles of equal mass are placed at 2015 vertices of the polygon. Find the distance of the centre of mass of the particle system from the centre of the polygon.
(ii) In the last problem you have been asked to remove any one particle from the system so that the centre of mass of the remaining 2014 particles lies farthest from the geometrical centre of the polygon. Which particle will you remove ?
View SolutionFind out the position of centre of mass of two particle system.
View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionThree equal masses each of 50 g, are placed at the corners of a right angled isoceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is
View Solution

