A disc rotating about its axis with angular speed ω0 is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are on the disc shown . Will the disc roll in the direction indicated?

We know that , υ=Rω
For point A,υA=Rω0(in the direction of the arrow)
For point B,υB=Rω0(in the direction opposite to arrow ) for point C,υC=(R2)ω0 (in the direction of the arrow). The disc will not roll in the direction indicated. it is because the disc is placed on a perfectely frictionless table and without friction, a body cannot roll.
Similar Questions
A disc roating about its axis with angular speed ω0 is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A,BandC on the disc shown in Fig. Will the disc roll in the direction indicated ?
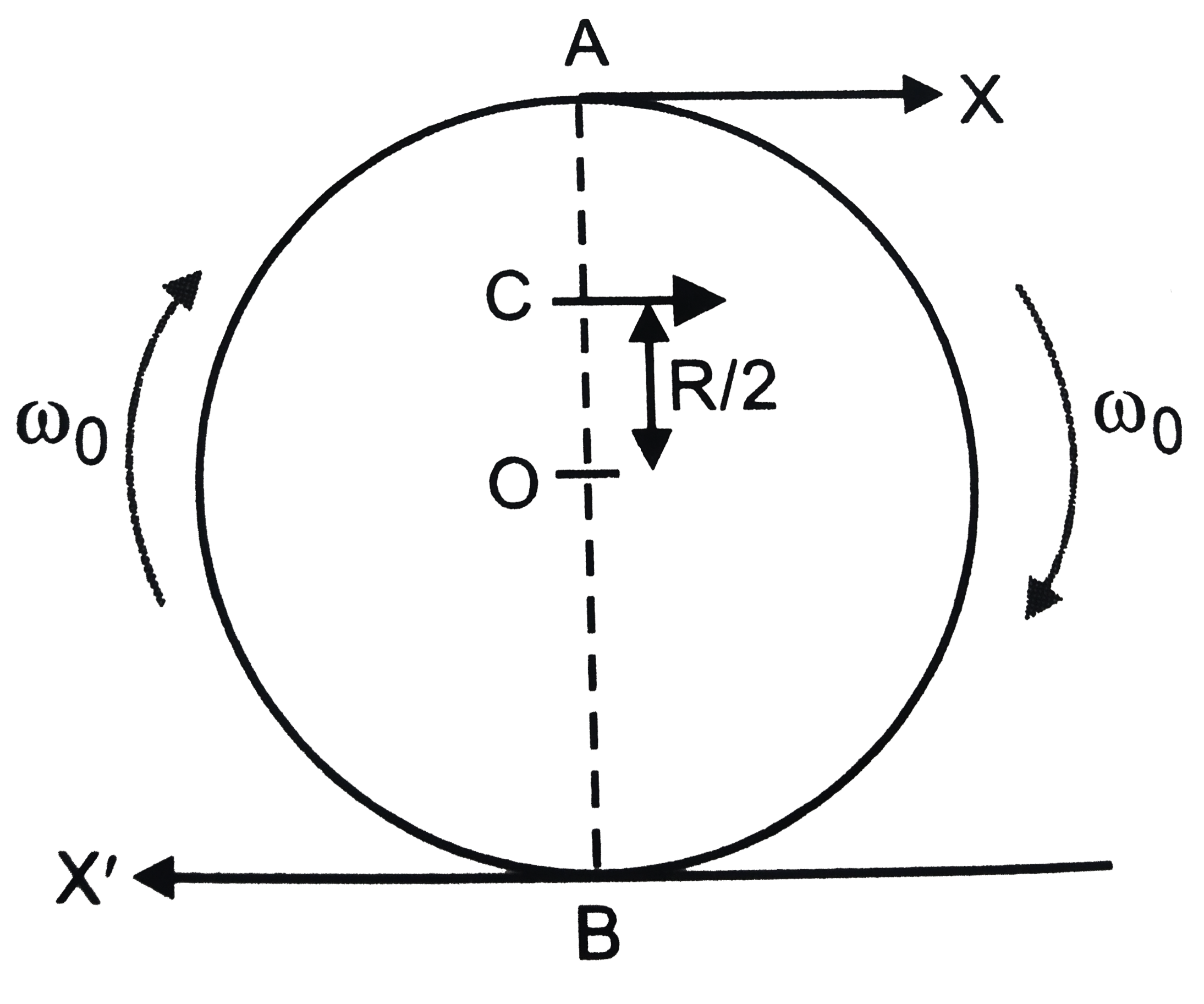
View SolutionA disc rotating about its axis with angular speed ω0 is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A,BandC on the disc shown in Fig. Will the disc roll in the direction indicated ?

View Solution
Knowledge Check
A brass disc is rotating about its axis. If temperature of disc is increased then its
Aradius of gyration increases, but moment of inertia remains the sameBmoment of inertia increases but radius of gyration remains the sameCradius of gyration, moment of inertia both remain the sameDradius of gyration, moment of inertia both increaseWhen a circular disc of radius 0.5 m is rotating about its own axis, then the direction of its angular momentum is
Aalong the tangent drawn at every pointBradialCperpendicular to the direction of angular velocityDalong the axis of rotation of the bodyA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
Aω6Bω3Cω2Dω5
A circular disc of mass M and radius R is rotating about its axis with angular speed If about another stationary disc having radius ω1.
R2 and same mass M is dropped co- axially on to the rotating disc. Gradually both discs attain constant angular speed ω2. The energy lost in the process is p% of the initial energy . Value of p is ........
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View SolutionA nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity ω . The magnt moment of this disc is .
View SolutionAssertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v.
Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.
View SolutionA circular disc is rotating without friction about its natural axis with an angular velocity ω. Another circular disc of same material and thickness but half the raduis is gently placed over it coaxially. The angular velocity of composite disc will be
View Solution

