A uniform piece of metal sheet is cut in the form as shown in the figure. Locate the centre of mass of the piece.
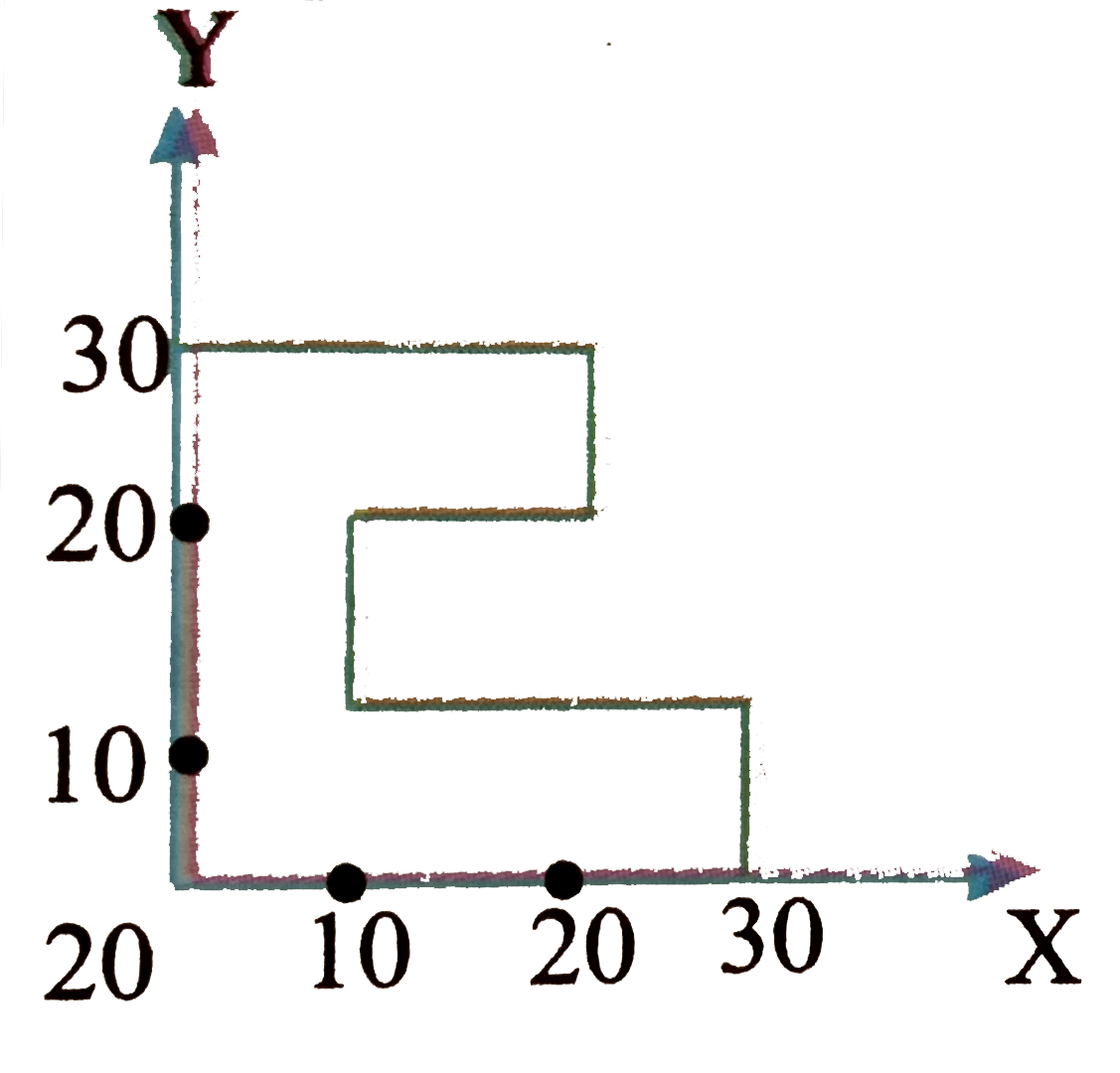
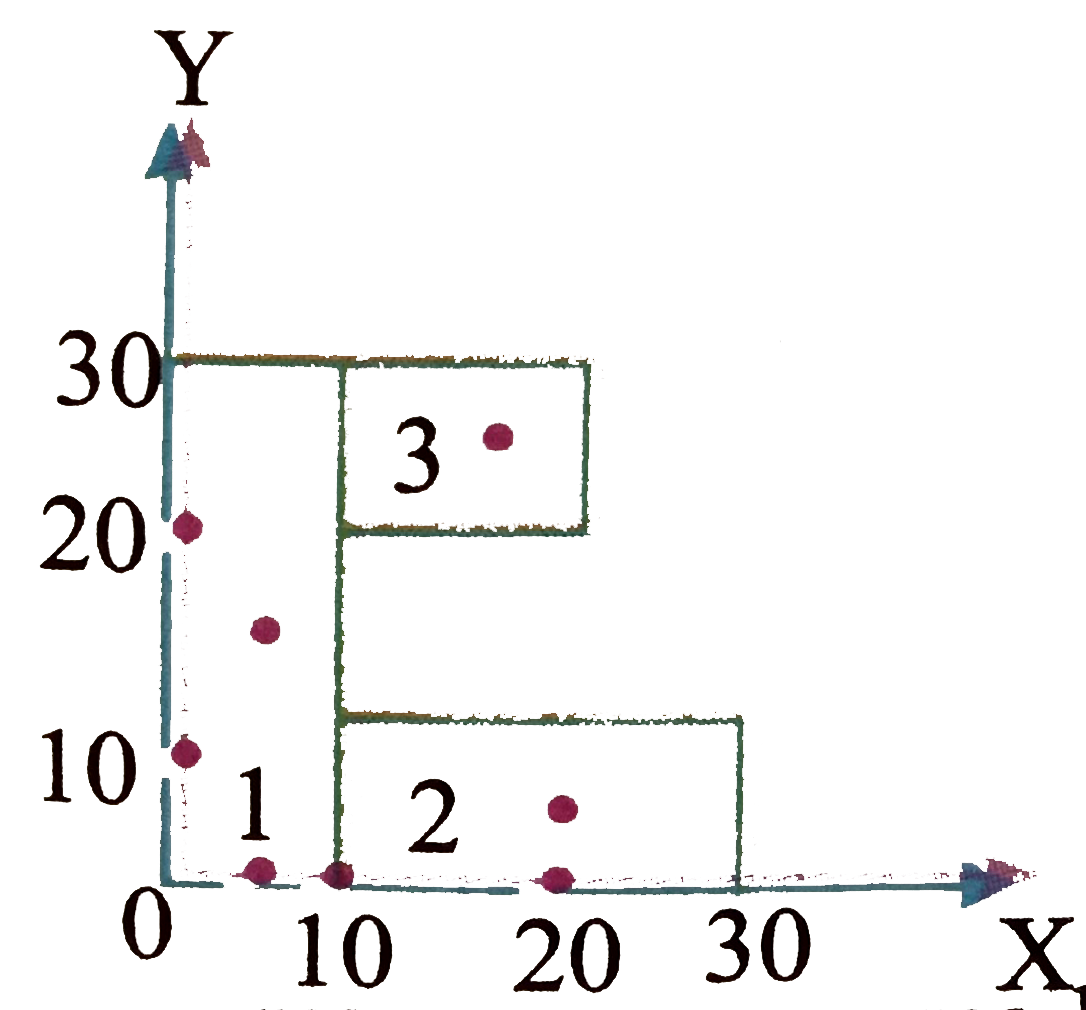
Let the mass per unit area be σ. We divide the structures into parts 1,2 and 3. The mass of part-1 is 300σ, mass of part -2 is 200σ and that of part −3 is 100σ. The coordinates of centre of mass of part 1 are (5,15), that of part (20,5) , and that of part −3 are (15,25).
Xcm=(300σ)5+(200σ)20+(100σ)15600σ≈11.7
Ycm=(300σ)15+(200σ)5+(100σ)12600σ≈13.3
In vector notation ¯rcm=11.7ˆi+13.3ˆj
Similar Questions
Knowledge Check
A uniform place of sheet is shaped as shown in the figure. Compute x and y co-ordinate of center of mass piece.
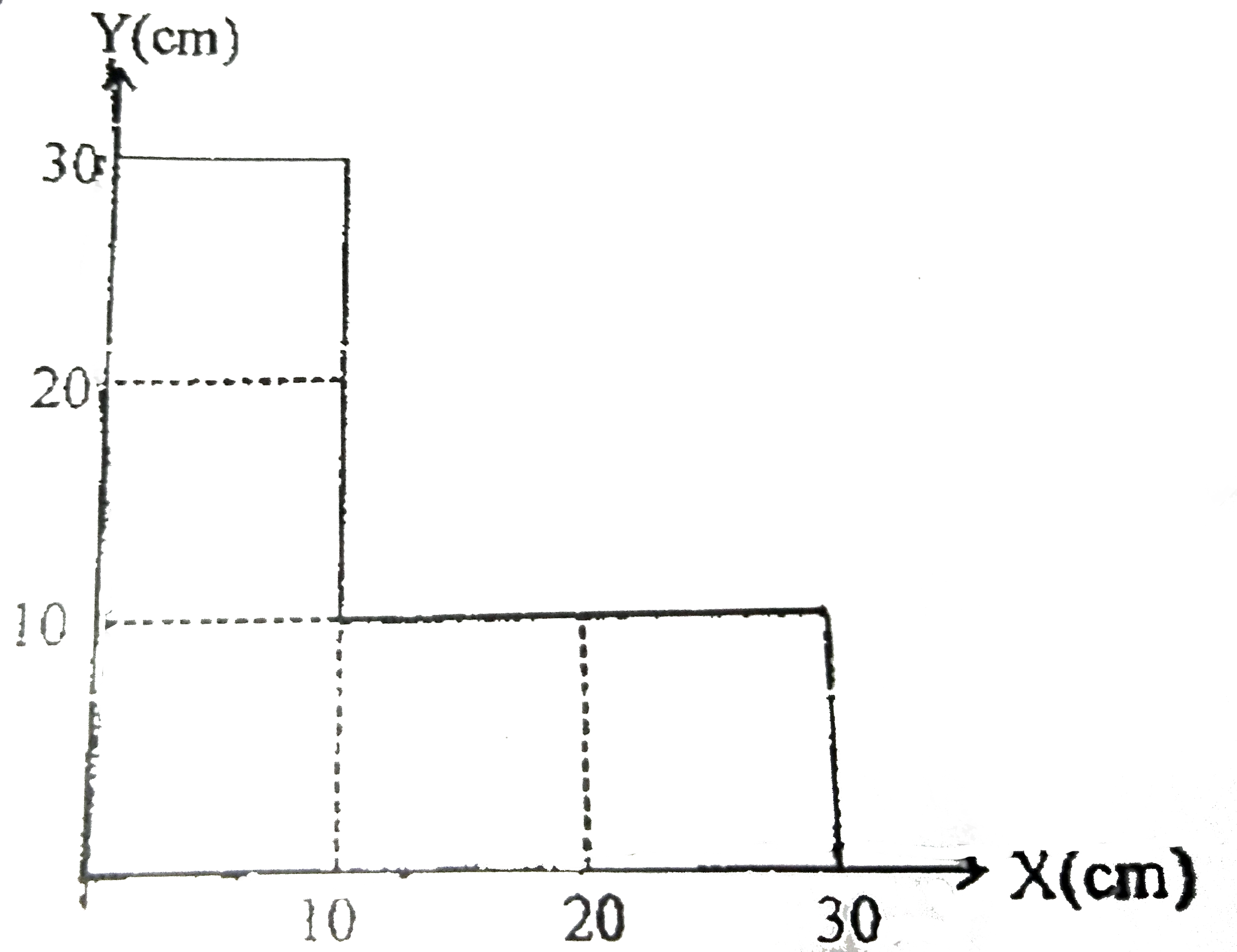 A11cm, 11cmB20cm,20cmC10cm,10cmD10cm,20cm
A11cm, 11cmB20cm,20cmC10cm,10cmD10cm,20cmFrom a 16cm×8cm rectangular uniform plane sheet, exactly one quarter of the sheet is removed as shown in figure. If the origin be taken at the centre of the sheet considered as shown in the figure the coordinates of the centre of mass of the remaining sheet is
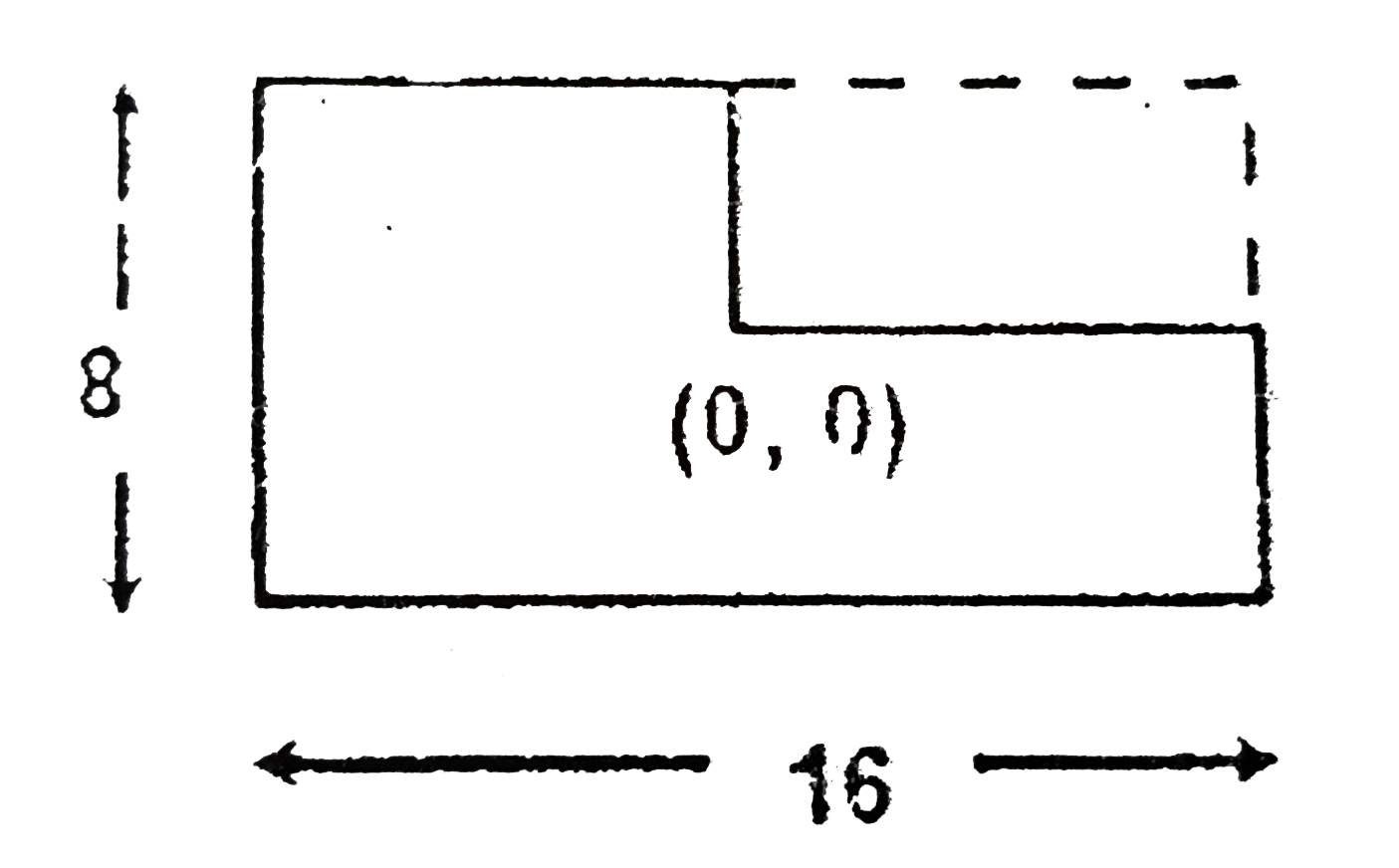 A(4/3,2/3)B(0,2/3)C(4/3,0)D(−4/3,−2/3)
A(4/3,2/3)B(0,2/3)C(4/3,0)D(−4/3,−2/3)A uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
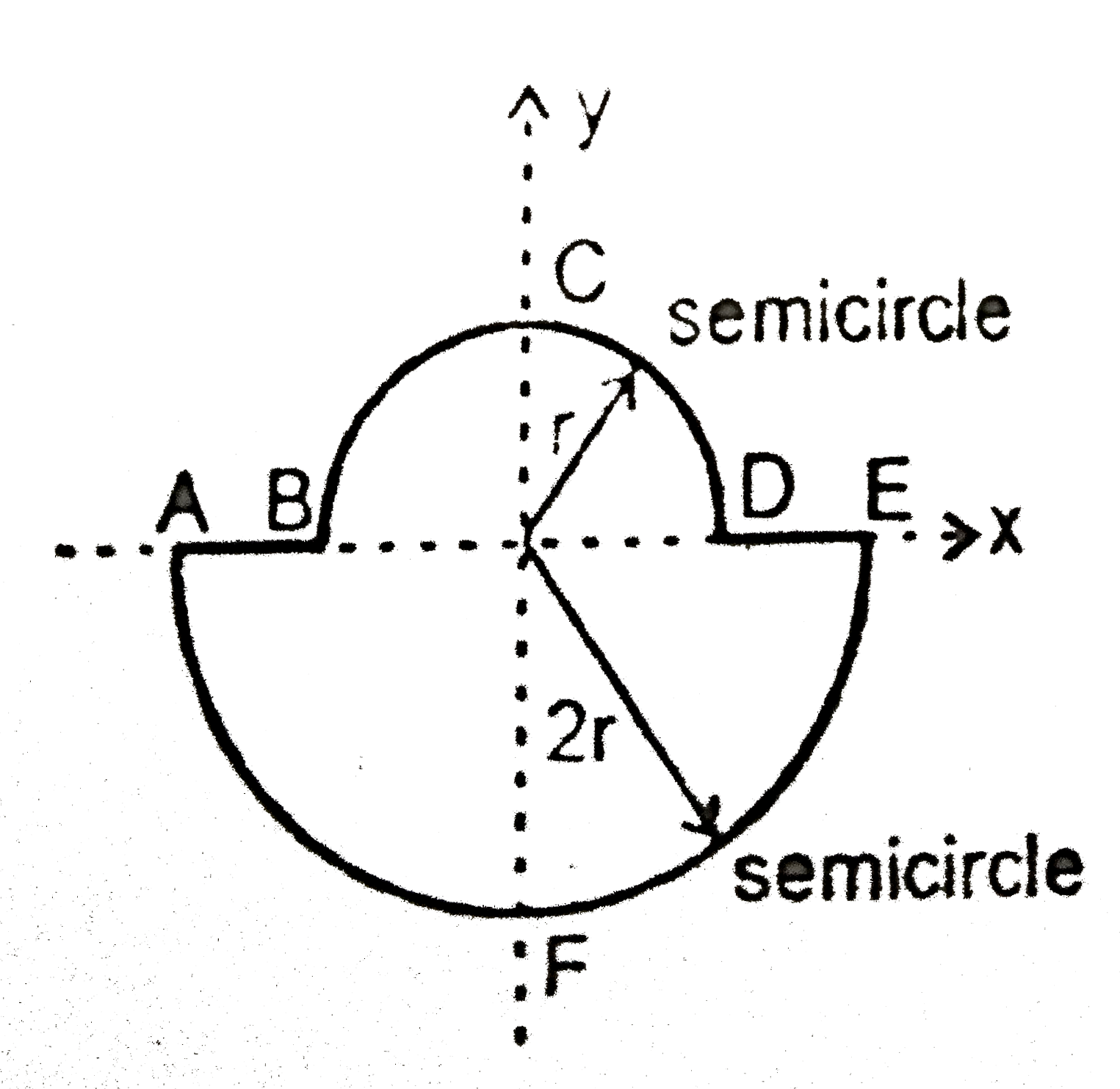 A2rπB−6r3π+2C−2rπDZero
A2rπB−6r3π+2C−2rπDZero
The given figure shows a square piece of carboard of side 10 inches. A rectangular piece of dimensions 3 inches × 2 inches is cut from the cardboard as shown in the figure.
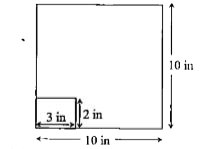
Area of the remaining portion of the cardboard is
View SolutionFrom a piece of paper in the shape of a regular hexagon, sectors of circles with the centre at the vertices are removed as shown in the figure. Find the fraction of the vertices are removed as shown in the figure. Find the fraction of the piece of paper left. Also find the perimeter of the piece of paper left in terms of a side of the hexagon

View SolutionCricket bat is cut at the location of its centre of mass as shown in the fig. Then

View SolutionA bar magnet has a pole strength 'K'. If it is cut into 4 pieces as shown in the figure. The pole strength of each piece now is ____

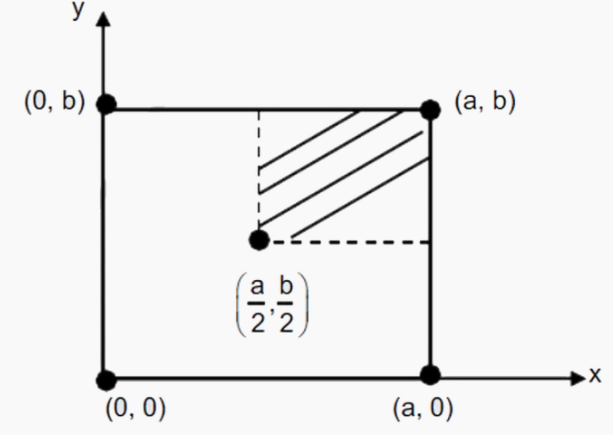
View SolutionFrom a rectangular sheet of uniform density a reactangle is cut out as shown in figure. Find new co-ordinate of center of mass w.r.t orign
View Solution