The curve between absolute temperature and v2rms is
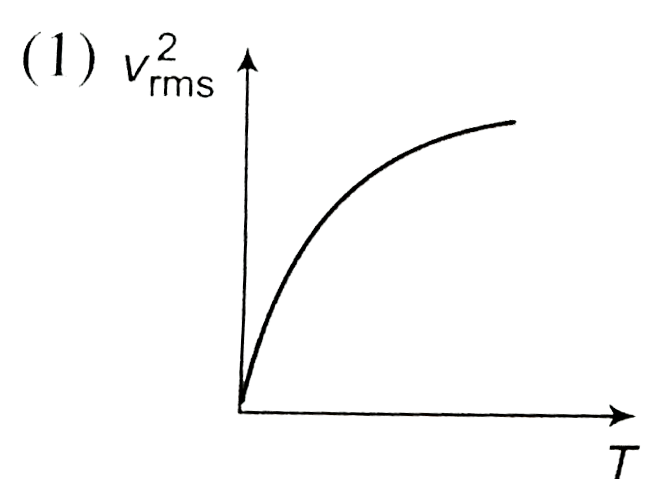
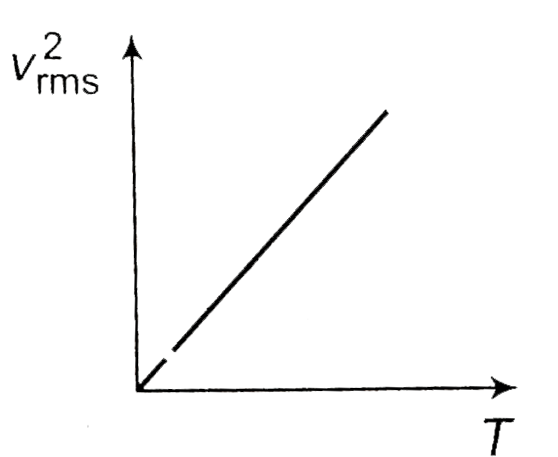
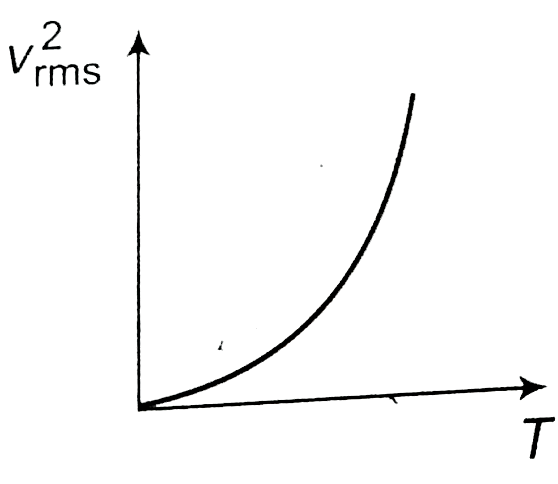
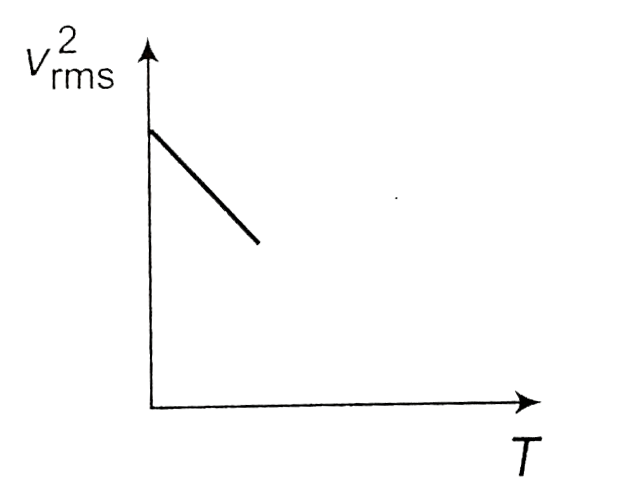
The correct Answer is:B
To find the relationship between absolute temperature (T) and the square of the root mean square speed (v_rms²), we can follow these steps:
1. Understand the Definition of v_rms:
The root mean square speed (v_rms) of gas molecules is given by the formula:
vrms=√3RTM
where R is the universal gas constant, T is the absolute temperature, and M is the molar mass of the gas.
2. Square the v_rms Expression:
To find the relationship between v_rms² and T, we square both sides of the equation:
v2rms=3RTM
3. Identify the Relationship:
From the equation v2rms=3RTM, we can see that v_rms² is directly proportional to T. This can be expressed as:
v2rms∝T
4. Conclusion about the Curve:
Since v_rms² is directly proportional to T, we can conclude that if we plot v_rms² against T, the graph will be a straight line passing through the origin. This indicates a linear relationship.
5. Final Answer:
Therefore, the curve between absolute temperature (T) and v_rms² is a straight line.
The root mean square speed (v_rms) of gas molecules is given by the formula:
vrms=√3RTM
where R is the universal gas constant, T is the absolute temperature, and M is the molar mass of the gas.
To find the relationship between v_rms² and T, we square both sides of the equation:
v2rms=3RTM
From the equation v2rms=3RTM, we can see that v_rms² is directly proportional to T. This can be expressed as:
v2rms∝T
Since v_rms² is directly proportional to T, we can conclude that if we plot v_rms² against T, the graph will be a straight line passing through the origin. This indicates a linear relationship.
Therefore, the curve between absolute temperature (T) and v_rms² is a straight line.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The absolute temperature of a gas
Ais a measure of number of molecules of the gasBindicates nature of the gasCis a measure of volume of the gasDnone of theseAbsolute zero temperature is
A0∘C,B100∘CC273.15∘cD−273.15∘CAbsolute zero temperature is
A0∘CB0 KC0∘FD273∘C

