A small source of sound vibrating at frequency 500Hz is rotated in a circle of radius 100/πcm at a constant angular speed of 5.0 revolutions per second. A listener situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air =332m/s.
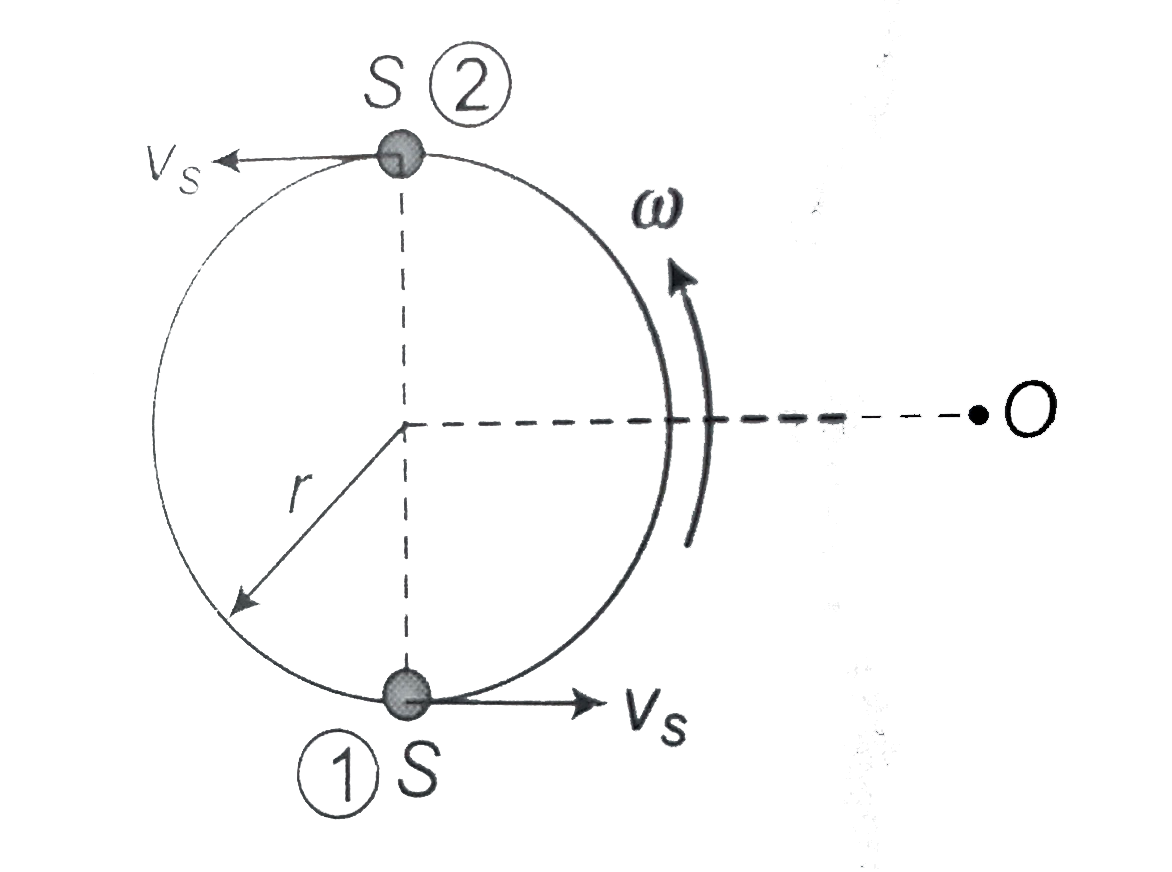
Speed of source vs=rω=1π×2π×5=10m/s,
Speed of sound v=332m/s
The listener will hear maximum frequency when source is in position ①
fmax=f(vv−vs)=500(322332−10)=516Hz
The listener will hear minimum frequency when source is in position ②
fmin=f(vv+vs)=500(322332−10)=485Hz
Topper's Solved these Questions
- SOUND WAVESBook:CP SINGHChapter:SOUND WAVESExercise:Exercises
Explore 130 Videos
- SIMPLE HARMONIC MOTIONBook:CP SINGHChapter:SIMPLE HARMONIC MOTIONExercise:Exercises
Explore 125 Videos
- TEMPERATURE AND THERMAL EXPANSIONBook:CP SINGHChapter:TEMPERATURE AND THERMAL EXPANSIONExercise:EXERCISES
Explore 64 Videos
Similar Questions
A source of sound of frequency 256 Hz is rotating in a circle of radius 3 m with angular speed of 20 rad/s. A listener is standing at rest along the line of centre of the circle. Under which position of the source of sound the listener will hear sound of
(a) maximum frequency
(b) minimum frequency
(c) same frequency as the frequency of source.
View SolutionA closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air =340ms−1.
View Solution
Knowledge Check
A small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For half the circle and smaller during the other half for an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will beAfmin=455Hz,fmax=535HzBfmin=484Hz,fmax=515HzCfmin=484Hz,fmax=500HzDfmin=500Hz,fmax=515HzA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. If the observer moves towards the source with a constant speed of 20ms, along the radial line to the centre, the fractional change in the apparent frequency over the frequency that the source will have if considered at reat at the centre will beA6%B3%C2%D9%A small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer situated at a great distance on a straight line perpendicular to the plane of the circle, through its centre, the apparent frequency of the source will beAgreater that 500 HxBsmaller than 500 HzCalways remain 500 HzDgreater for half the circle and smaller during the other half
A whistle of frequency 540Hz is moving in a circle of radius 2 ft at a constant angular speed of 15 rad//s. What are the lowest and height frequencies heard by a listener standing at rest, a long distance away from the centre of the circle? (velocity of sound in air is 1100ft/sec.)
View SolutionA whistle of frequency 540 Hz is moving in a circle of radius 2 ft at a constant angular speed of 15 rad/s. What are the lowest and highest frequencies heard by a listener standing at rest, a long distance away from the centre of the circle? (Velocity of sound in air is 1100ft/s)
View SolutionA person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360ms−1.
View SolutionA whistle of frequency 385Hz rotates in a horizontal circle of radius 50cm at an angular speed of 20 radians s−1 the lowest frequency heard by a listener a long distance way at rest with velocity to the centre of the circle given velocity of sound equal to 340ms−1 is
View SolutionFind the fundamental frequency of a closed pipe, if the length of the air column is 42 m . (speed of sound in air = 332 m/sec )
View Solution

