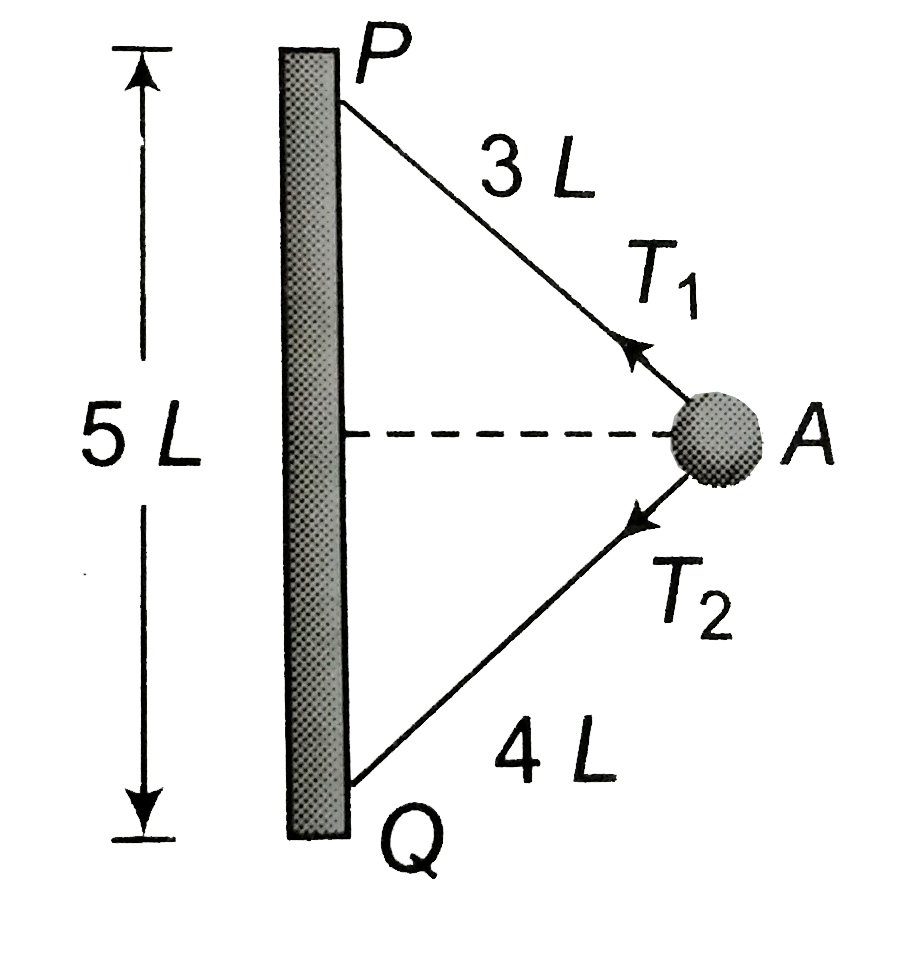
A particle A of mass m is attached to a vertical axis by two stings PA and QA of lengths 3L and 4L , respectively. PQ=5L. A rotates around the axis with an angular speed ω. The tension in the two strings are T1 and T2.
(i) T1=T2
(ii) 3T1−4T2=5mg
(iii) 4T1+3T2=12mω2L
A
(i)only
B
(i),(ii)
C
(i),(iii)
D
(ii),(iii)
Video Solution
Text Solution
The correct Answer is:D
∠PAQ=90∘
Sinα=45,cosα=35
sinβ=35,cosβ=45
r=3Lsinα=12L5
T1cosα=T2cosβ+mg
T1×35=T2×45+mg
3T1−4T2=5mg
T1×45+T2×35=mω2(12L5)
4T1+3T2=12mω2L


|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
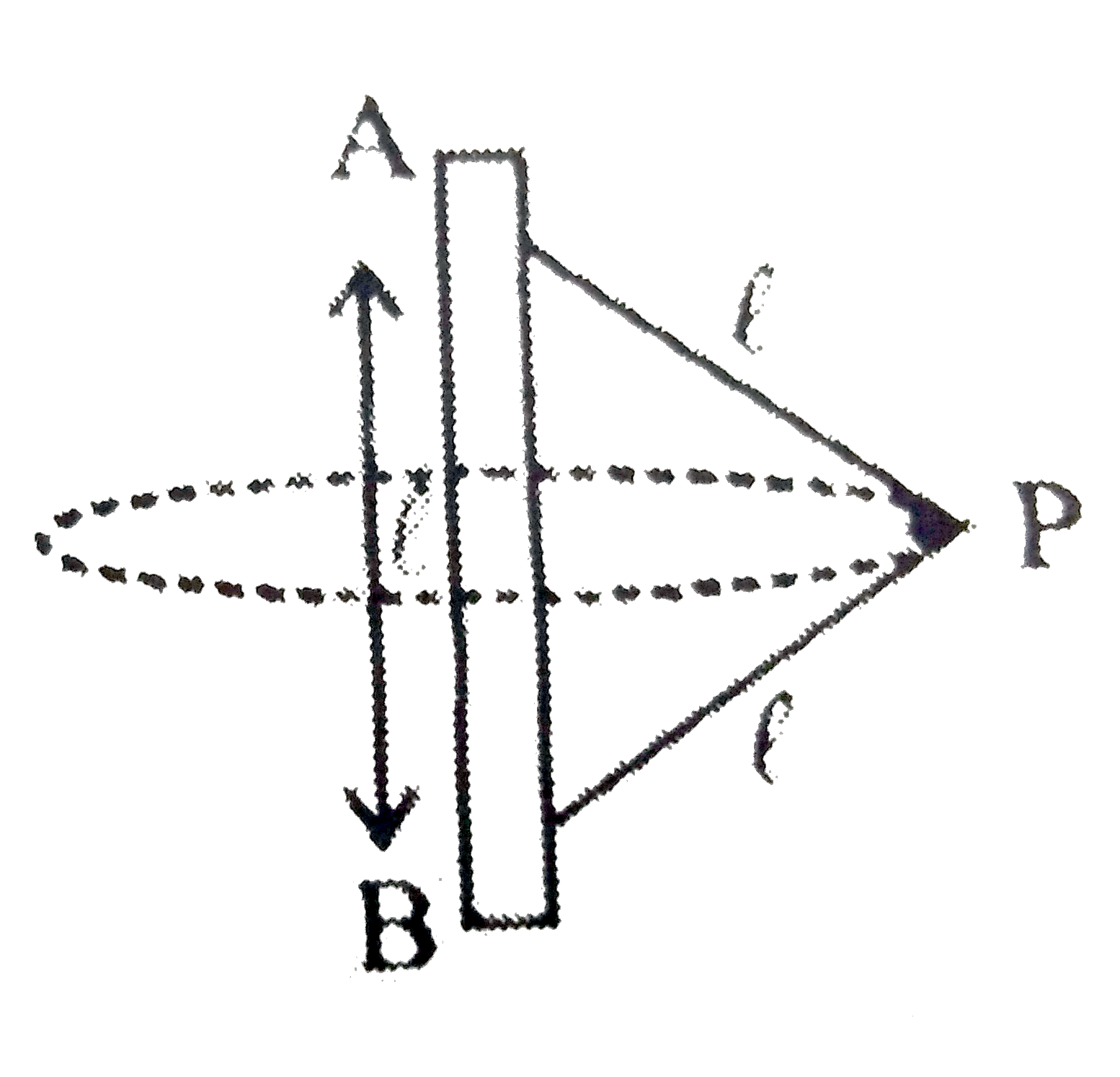 AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remain taut only if ω≥√2gl
AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remain taut only if ω≥√2glA particle P of mass m is attached to a vertical axis by two strings AP and BP of legth l each. The separation AB=l, rotates around the axis with an angular velocity ω. The tension in the two string are T1 and T2. Then
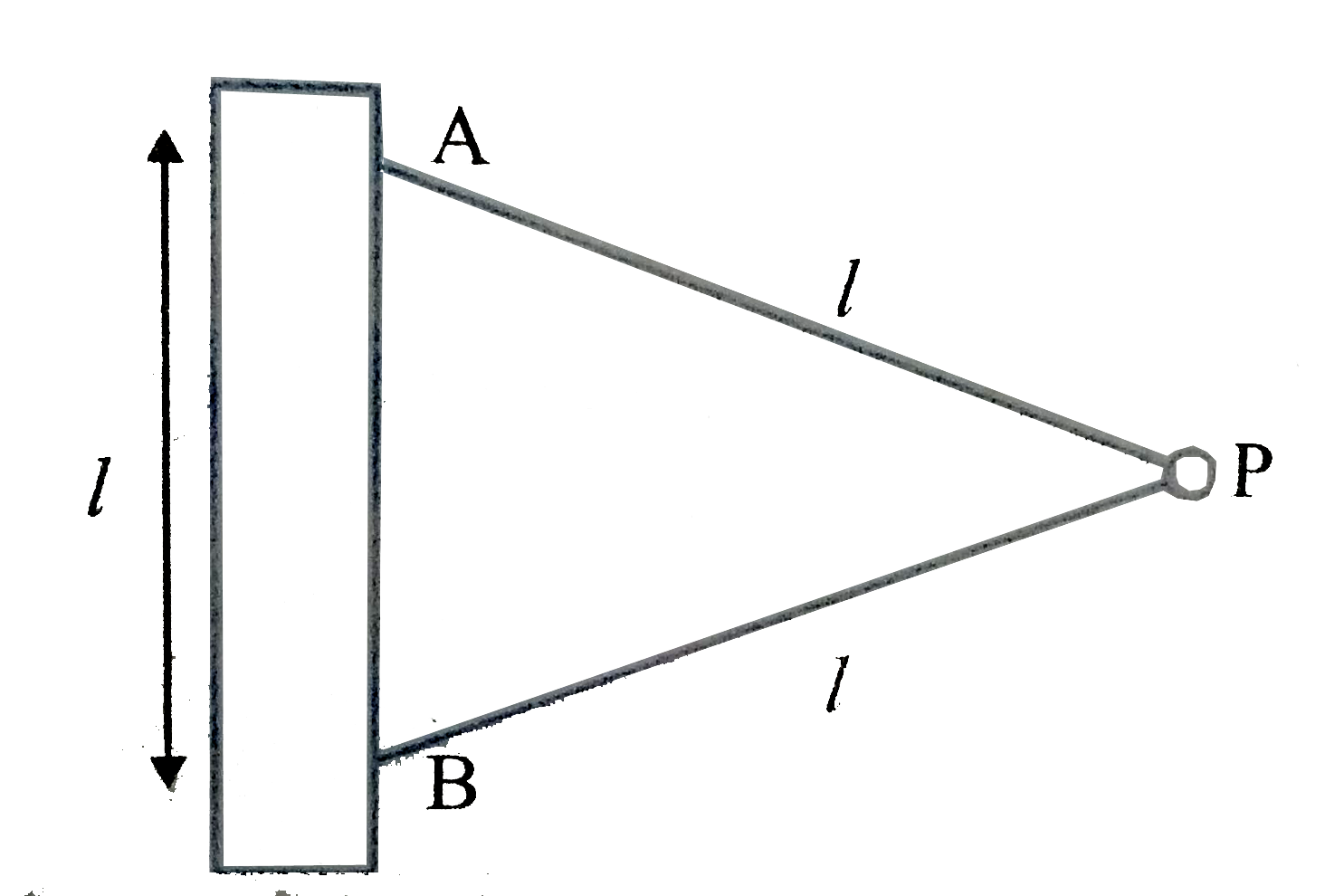 AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remains taut only if ω≥√2g/l
AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remains taut only if ω≥√2g/lA uniform rod of mass m and length L is suspended with two massless strings as shown in figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1/T2 is
 A1:1B1:2C2:1D4:3
A1:1B1:2C2:1D4:3
Two particles each of mass m are moving in horizontal circle with same angular speed. If both string are of same length then the ratio of tension in string T1T2 is
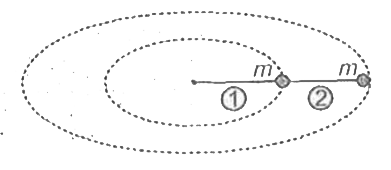
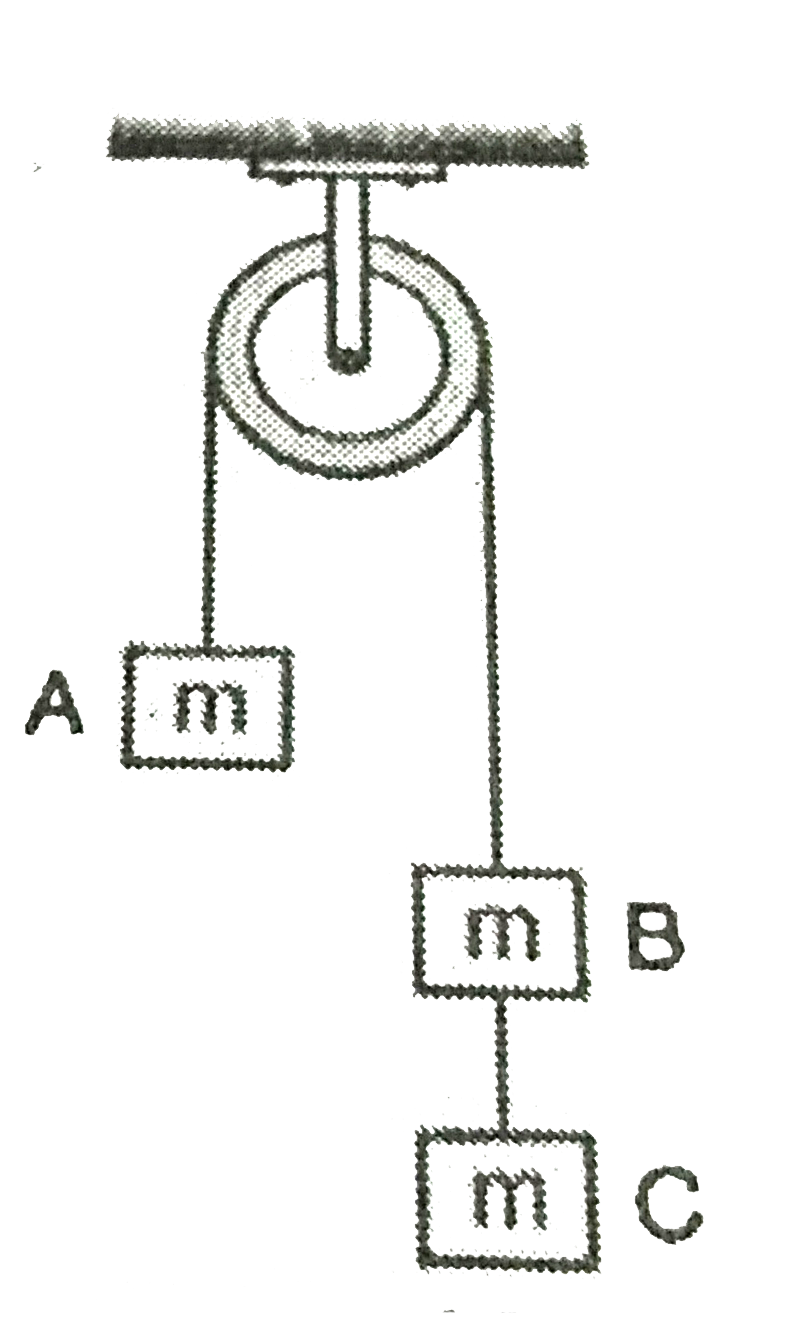
View SolutionIn fig tension in the string that connects the masses A and B is T1 and that in the string connecting B and C is T2 then T1T2 is:
View SolutionIn an A.P. if S1=T1+T2+T3+…+Tn (n odd) S2=T1+T3+T5+…+Tn, then S1/S2 =
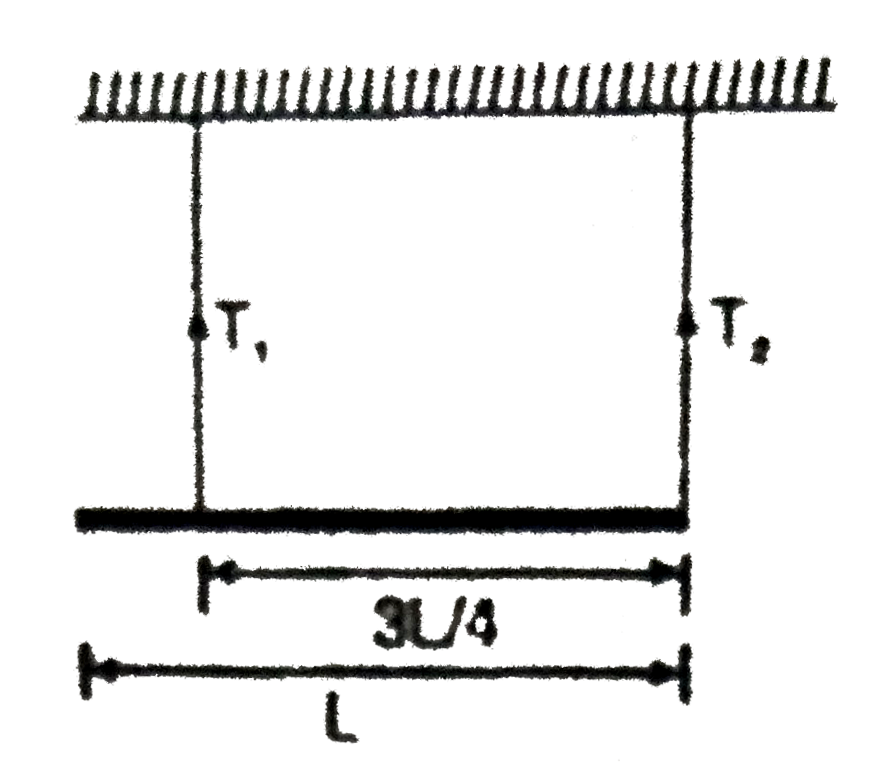
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
View Solution

