A U-tube is filled with mercury. When two limbs are maintained at temperatures of 0∘C and 100∘C , then heights of the two columns are 100cm and 101.8cm . What is the real coefficient of cubical expansion of mercury ? (Expansion of vessel may be neglected)
To find the real coefficient of cubical expansion of mercury, we will follow these steps:
Step 1: Understand the problem
We have a U-tube filled with mercury, where one limb is at 0°C and the other at 100°C. The heights of the mercury columns are given as 100 cm and 101.8 cm, respectively. We need to find the real coefficient of cubical expansion (γ) of mercury.
Step 2: Apply pressure equilibrium
Since both limbs are open to the atmosphere, we can use the principle of pressure equilibrium. The pressure at the same horizontal level in both limbs must be equal.
Let:
- P0 = atmospheric pressure
- ρ0 = density of mercury at 0°C
- ρ100 = density of mercury at 100°C
- H1=100cm (height of mercury column at 0°C)
- H2=101.8cm (height of mercury column at 100°C)
The pressure at the first limb is:
P0+ρ0gH1
The pressure at the second limb is:
P0+ρ100gH2
Setting these equal gives us:
P0+ρ0gH1=P0+ρ100gH2
Step 3: Simplify the equation
Cancel P0 and g from both sides:
ρ0H1=ρ100H2
Step 4: Relate densities using the coefficient of cubical expansion
The density of mercury at 100°C can be expressed in terms of the density at 0°C using the formula:
ρ100=ρ01+γΔT
where ΔT=100°C−0°C=100°C.
Substituting this into our equation gives:
ρ0H1=(ρ01+γ⋅100)H2
Step 5: Cancel ρ0 and rearrange
Cancel ρ0 from both sides:
H1=H21+γ⋅100
Rearranging gives:
1+γ⋅100=H2H1
Step 6: Substitute the values of H1 and H2
Substituting H1=100cm and H2=101.8cm:
1+γ⋅100=101.8100
Step 7: Solve for γ
Calculating the right side:
1+γ⋅100=1.018
Subtracting 1 from both sides:
γ⋅100=0.018
Dividing by 100 gives:
γ=0.018100=1.8×10−4per degree Celsius
Final Answer
The real coefficient of cubical expansion of mercury is:
γ=1.8×10−4per degree Celsius
---
We have a U-tube filled with mercury, where one limb is at 0°C and the other at 100°C. The heights of the mercury columns are given as 100 cm and 101.8 cm, respectively. We need to find the real coefficient of cubical expansion (γ) of mercury.
Since both limbs are open to the atmosphere, we can use the principle of pressure equilibrium. The pressure at the same horizontal level in both limbs must be equal.
- P0 = atmospheric pressure
- ρ0 = density of mercury at 0°C
- ρ100 = density of mercury at 100°C
- H1=100cm (height of mercury column at 0°C)
- H2=101.8cm (height of mercury column at 100°C)
P0+ρ0gH1
P0+ρ100gH2
P0+ρ0gH1=P0+ρ100gH2
Cancel P0 and g from both sides:
ρ0H1=ρ100H2
The density of mercury at 100°C can be expressed in terms of the density at 0°C using the formula:
ρ100=ρ01+γΔT
where ΔT=100°C−0°C=100°C.
ρ0H1=(ρ01+γ⋅100)H2
Cancel ρ0 from both sides:
H1=H21+γ⋅100
1+γ⋅100=H2H1
Substituting H1=100cm and H2=101.8cm:
1+γ⋅100=101.8100
Calculating the right side:
1+γ⋅100=1.018
γ⋅100=0.018
γ=0.018100=1.8×10−4per degree Celsius
The real coefficient of cubical expansion of mercury is:
γ=1.8×10−4per degree Celsius
Topper's Solved these Questions
- TEMPERATURE AND THERMAL EXPANSIONBOOK - CP SINGHCHAPTER - TEMPERATURE AND THERMAL EXPANSIONEXERCISE - EXERCISES
64 Videos
- SOUND WAVESBOOK - CP SINGHCHAPTER - SOUND WAVESEXERCISE - Exercises
130 Videos
- UNITS, DIMENIONS AND MEASUREMENTSBOOK - CP SINGHCHAPTER - UNITS, DIMENIONS AND MEASUREMENTSEXERCISE - Exercises
63 Videos
Similar Questions
Two vessel connected by a pipe with a sliding plug contain mercury. In one vessel, the height of murcury column is 39.2cm and its temperature is 0∘C, while in the other, the height of mercury column is 40cm and its temperature is 100∘C. Find the coefficient if cubical expansion for mercury. The volume of the connecting pipe should be neglected.
View SolutionA barometer having a brass scale reads 77.24 cm at a temperature of 20∘C. The scale is graduated to be accurate at 0∘C. What would be the readint at 0∘C ? Coefficient of cubical expansion of mercury =18×10−5.∘C−1 and linear expansion of brass −19×10−6.∘C−1
View Solution
Knowledge Check
The density of a liquid at 100∘C is 8.0g/cm3 and at 0∘C is 8.4g/cm3, the coefficient of cubical expansion of the liquid is
A10−4/∘CB5×10−4/∘CC8×10−4/∘CD4×10−4/∘CA metal rod of silver at 0∘C is heated to 100∘C . It's length is increased by 0.19cm . Coefficient of cubical expansion of the silver rod is
A5.7×10−5/∘CB0.63×10−5/∘CC1.9×10−5/CD16.1×10−5/∘CA sphere of diameter 8cm and mass 275g floats in a bath of liquid. As the temperature is raised, the sphere begins to sink at a temperature of 400C. If the density of the liquid is 1.5g/cm3 at 00C, find the coefficient of cubical expansion of the liquid. Neglect the expansion of the sphere
A12×10−4/0CB25×10−4/0CC15×10−4/0CD115×10−4/0C
A sphere of radius 3.5 cm and mass 250 gm floats in a liquid at 20∘C. As the temperature is raised, the sphere just being to sink at a temperature of 35∘C. If the density of liquid at 0∘C is 1.527gm/cm3 find the coefficient of cubical expansion of the liquid. Neglect expansion of the sphere.
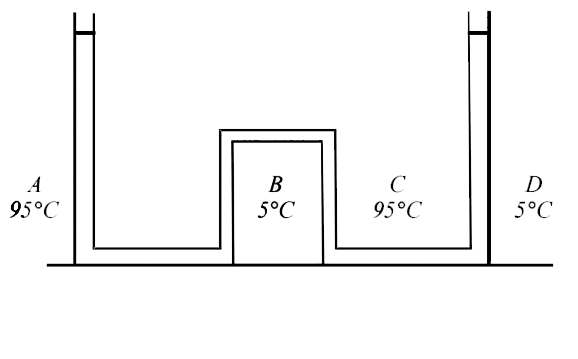
View SolutionThe apparatus shown in the figure consists of four glass columns connected by horizontal section. The height of two central column B and C are 49 cm each. The two outer columns A and D are open to the temperature. A and C are maintained at a temperature of 95∘C while the columns B and D are maintained at 5∘C. The height of the liquid in A and D measured from the base the are 52.8 cm and 51cm respectively. Determine the coefficient of thermal expansion of the liquid
View SolutionA weight thermometer contains 51g of mercury at 200C and 50g of mercury at 1000C. The coefficient of apparent expansion of mercury in glass vessel is
View SolutionA vertical column 50 cm long at 50∘C balances another column of same liquid 60 cm long at 100∘C . The coefficient of absolute expansion of the liquid is
View SolutionA glass bulb of volume 250cc is filled with mercury at 20∘C and the temperature is raised to 100∘C. If the coefficient of linear expansion of glass is 9×10−6/∘C). Coefficient of absolute expansion of mercury is 18×10−5/∘C). The volume of mercury overflows
View Solution
