A projectile is fired from the top of an 80 m high cliff with an initial speed of 30(m)/(s) at an unknown angle. The speed when its hits the ground.
50(m)/(s)
100(m)/(s)
45(m)/(s)
20(m)/(s)
The correct Answer is:A
To solve the problem of finding the speed of a projectile when it hits the ground after being fired from the top of an 80 m high cliff with an initial speed of 30 m/s, we can apply the principle of conservation of mechanical energy. Here’s the step-by-step solution:
Step 1: Understand the problem
We have a projectile fired from a height (h) of 80 m with an initial speed (u) of 30 m/s. We need to find the final speed (v) just before it hits the ground.
Step 2: Identify the energies at the two points
- At point A (the top of the cliff):
- Kinetic Energy (KE_A) = (1/2) * m * u²
- Potential Energy (PE_A) = m * g * h
- At point B (just before hitting the ground):
- Kinetic Energy (KE_B) = (1/2) * m * v²
- Potential Energy (PE_B) = 0 (since we take the ground level as the reference point)
Step 3: Apply the conservation of mechanical energy
According to the conservation of mechanical energy:
KEA+PEA=KEB+PEB
Substituting the expressions for kinetic and potential energy:
12mu2+mgh=12mv2+0
Step 4: Simplify the equation
We can cancel the mass (m) from all terms since it appears in every term:
12u2+gh=12v2
Step 5: Rearrange the equation to solve for v
Rearranging gives:
12v2=12u2+gh
Multiplying through by 2:
v2=u2+2gh
Step 6: Substitute the known values
- Initial speed, u=30m/s
- Height, h=80m
- Acceleration due to gravity, g=10m/s2
Now substituting these values into the equation:
v2=(30)2+2⋅10⋅80
v2=900+1600
v2=2500
Step 7: Calculate the final speed
Taking the square root of both sides:
v=√2500
v=50m/s
Final Answer
The speed of the projectile when it hits the ground is 50 m/s.
---
We have a projectile fired from a height (h) of 80 m with an initial speed (u) of 30 m/s. We need to find the final speed (v) just before it hits the ground.
- At point A (the top of the cliff):
- Kinetic Energy (KE_A) = (1/2) * m * u²
- Potential Energy (PE_A) = m * g * h
- At point B (just before hitting the ground):
- Kinetic Energy (KE_B) = (1/2) * m * v²
- Potential Energy (PE_B) = 0 (since we take the ground level as the reference point)
According to the conservation of mechanical energy:
KEA+PEA=KEB+PEB
12mu2+mgh=12mv2+0
We can cancel the mass (m) from all terms since it appears in every term:
12u2+gh=12v2
Rearranging gives:
12v2=12u2+gh
Multiplying through by 2:
v2=u2+2gh
- Initial speed, u=30m/s
- Height, h=80m
- Acceleration due to gravity, g=10m/s2
v2=(30)2+2⋅10⋅80
v2=900+1600
v2=2500
Taking the square root of both sides:
v=√2500
v=50m/s
The speed of the projectile when it hits the ground is 50 m/s.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A projectile is fired horizontally with an initial speed of 20 m/s/ its horzontal speed 3 sec later is:
A20m/sB6.67m/sC60m/sD29.4m/sA woman stands on the edge of a cliff and throws a stone vertically downward with an initial speed of 10 m/s. The instant before the stone hits the ground below, it has 450 J of kinetic energy. If she were to throw the stone horizontally outward from the cliff with the same initial speed of 10 m/s, how much kinetic energy would it have just before it hits the ground ?
A50JB100JC450JD800JA shell is fired with a horizontal velocity in the positive x direction from the top of an 80 m high cliff. The shell strikes the ground 1330 m from the base of the cliff. The drawing is not to scale.
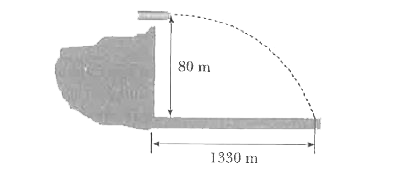
What is the speed of the shell as it hits the ground?A4.0 m/sB330 m/sC9.8 m/sD170 m/s
Statement -1 : Two projectiles are launched from the top of a cliff with same initial speed with different angles of projection. They reach the ground with the same speed. Statement -2 : The work done by gravity is same in both the case
View SolutionA projectile is fired vertically from the earth's surface with an initial speed of 10km/s. Neglecting air drag, how high above the surface of earth will it go?
View SolutionA 24−kg projectile is fired at an angle of 53∘ above the horizontal with an initial speed of 50m/s. At the highest point in its trajectory, the projectile explodes into two fragments of equal mass, the first of which falls vertically with zero initial speed.
(a) How far from the point of firing does the second fragment strike the ground? (Assume the ground is level.)
(b) How much energy was released during the explosion?
View SolutionA particle is dropped from the top of a tower of height 80m. Find the time of jurney and the speed with which it strikes the ground.
View SolutionA shell is fired with a horizontal velocity in the positive x direction from the top of an 80 m high cliff. The shell strikes the ground 1330 m from the base of the cliff. The drawing is not to scale.
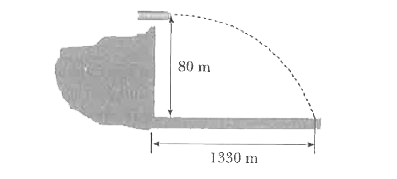
What is the magnitude of the acceleration of the shell just before is strikes the ground?
View Solution