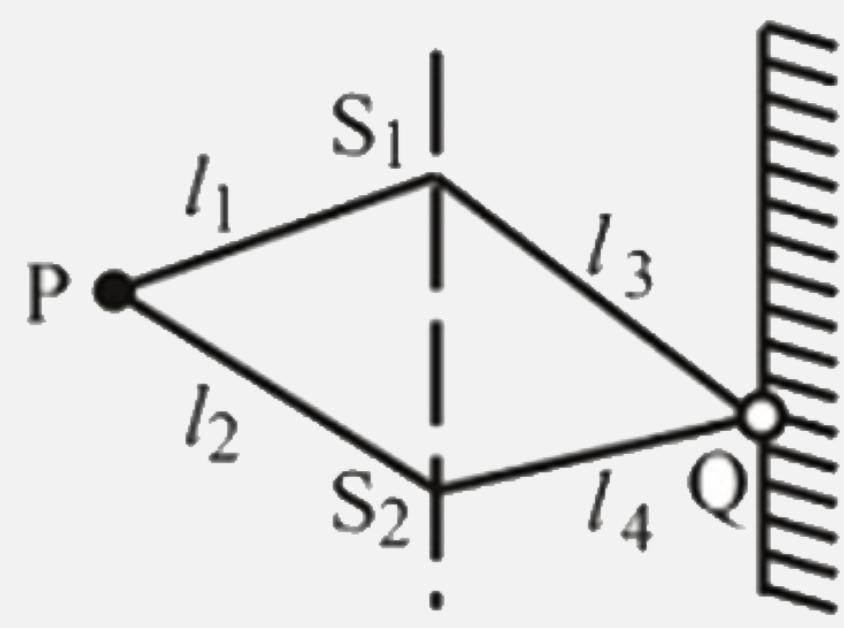
Two identical narrow slits S1 and S2 are illuminated by light of wavelength λ from a point source P. If, as shown in the diagtam above the light is then allowed to fall on a scree, and if n is a positive integer, the condition for destructive interference at Q is that

(l1−l2)=(2n+1)λ/2
(l3−l4)=(2n+1)λ/2
(l1+l2)−(l2+l4)
(l1+l3)−(l2+l4)=(2n+1)λ/2
The correct Answer is:D
Path difference=(l1+l3)−(l2−l4)
for distructive interfernce
Path difference =(2n+1)λ/2
from(1)&(2)
(l1+l3)−(l2−l4)=(2n+1)λ/2
Similar Questions
Two identical narrow slits S1andS2 are illuminated by the light of a wavelengthλ from a point source P. If , as shown in the diagram above , the light is then allowed to fall on a screen , and if n is a positive integer , the condition for destructive interference at Q is
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
A(a) Their phase differences remain constantB(b) Their phases are distributed randomlyC(c) Their light intensities remain constantD(d) Their light intensities change randomly - Question 2 - Select One
Two ideal slits S1 and S2 are at a distance d apart, and illuninated by light of wavelength λ passing through an ideal source slit S placed on the line through S2 as shown. The distance between the planes of slits and the source slit is D.A screen is held at a distance D from the plane of the slits. The minimum value of d for which there is darkness at O is (d<<D)
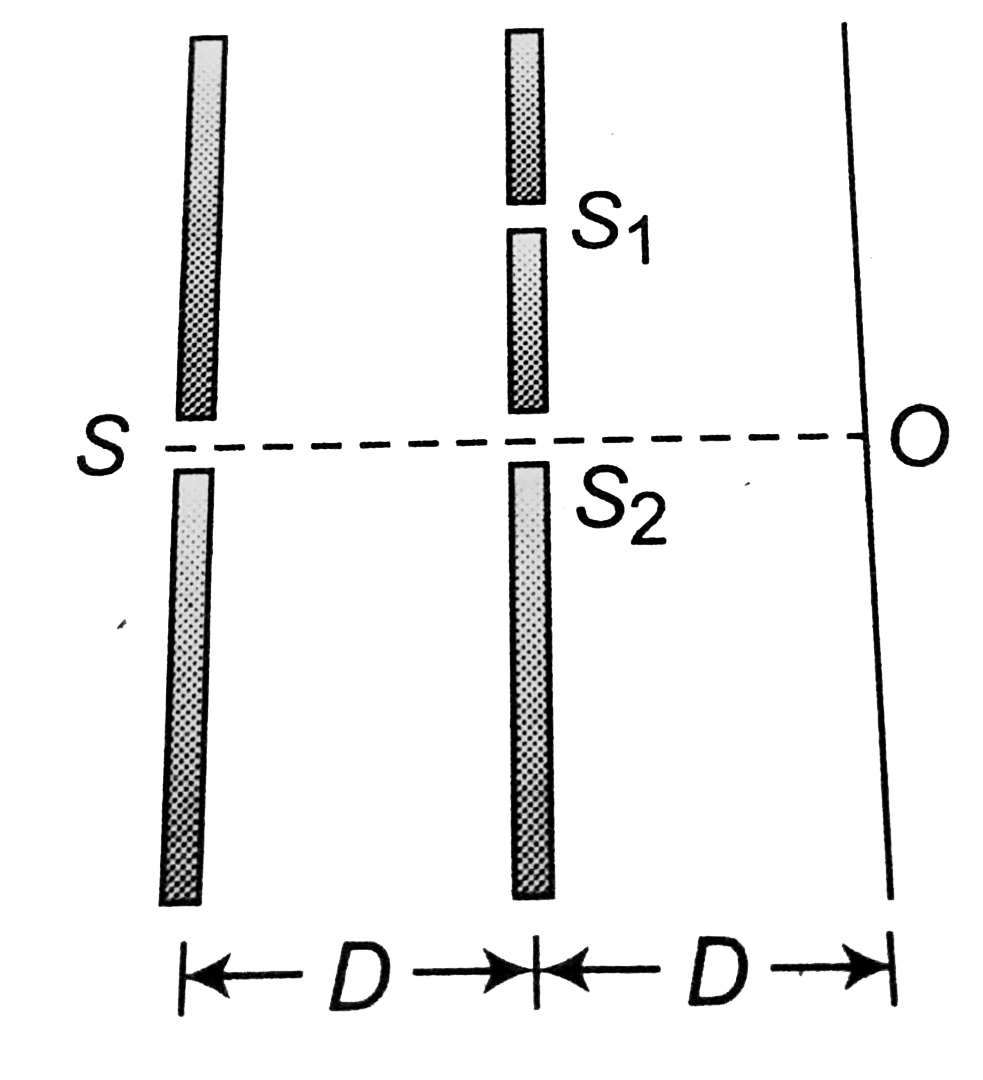 A√3λD2B√λDC√λD2D√3λD
A√3λD2B√λDC√λD2D√3λD - Question 3 - Select One
Choose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
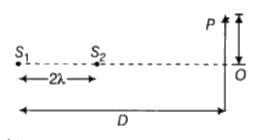 A√2DB√3DC√8DD√5D
A√2DB√3DC√8DD√5D
Consider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d
 View Solution
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
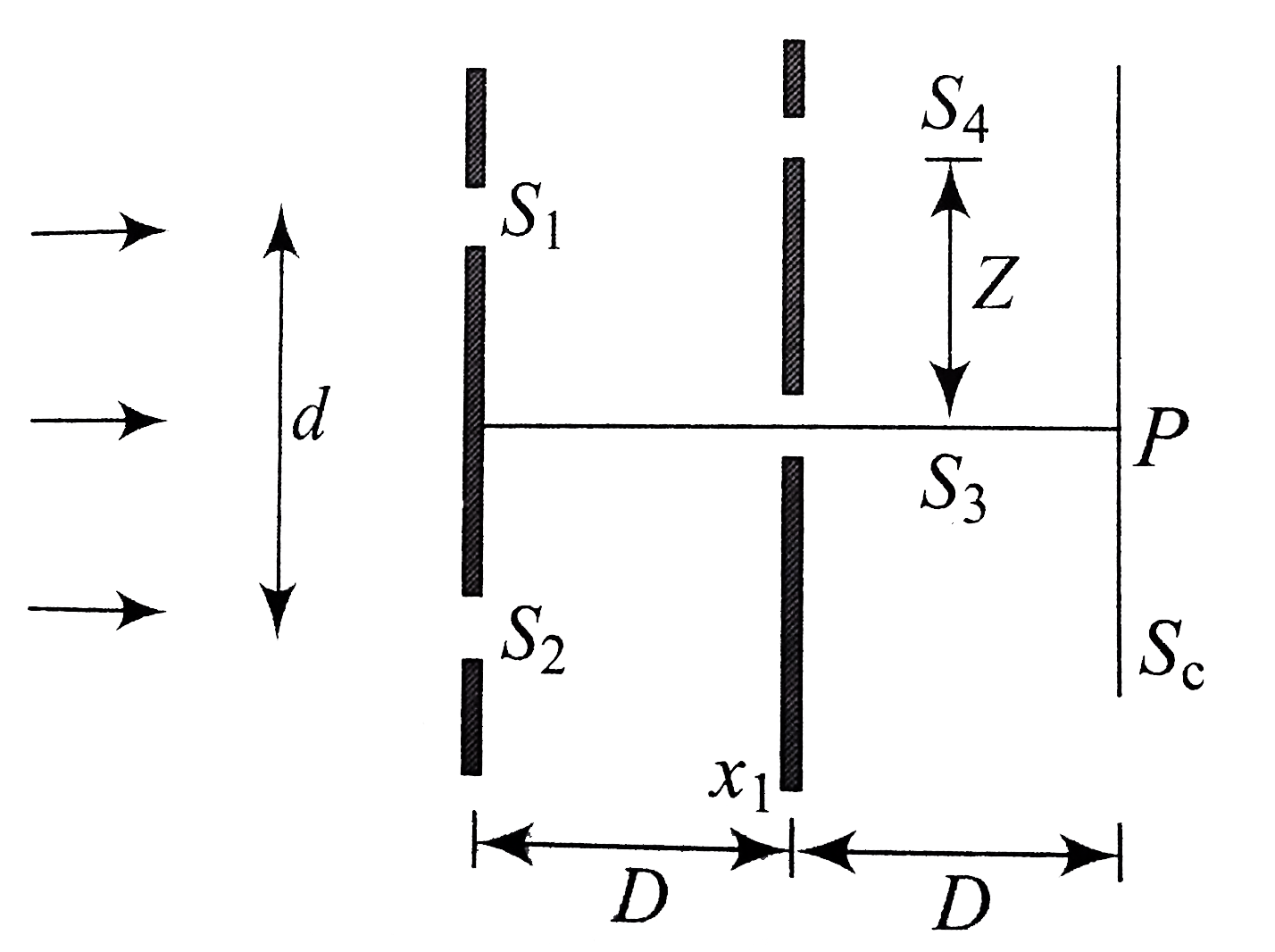
If z=λD2dView SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
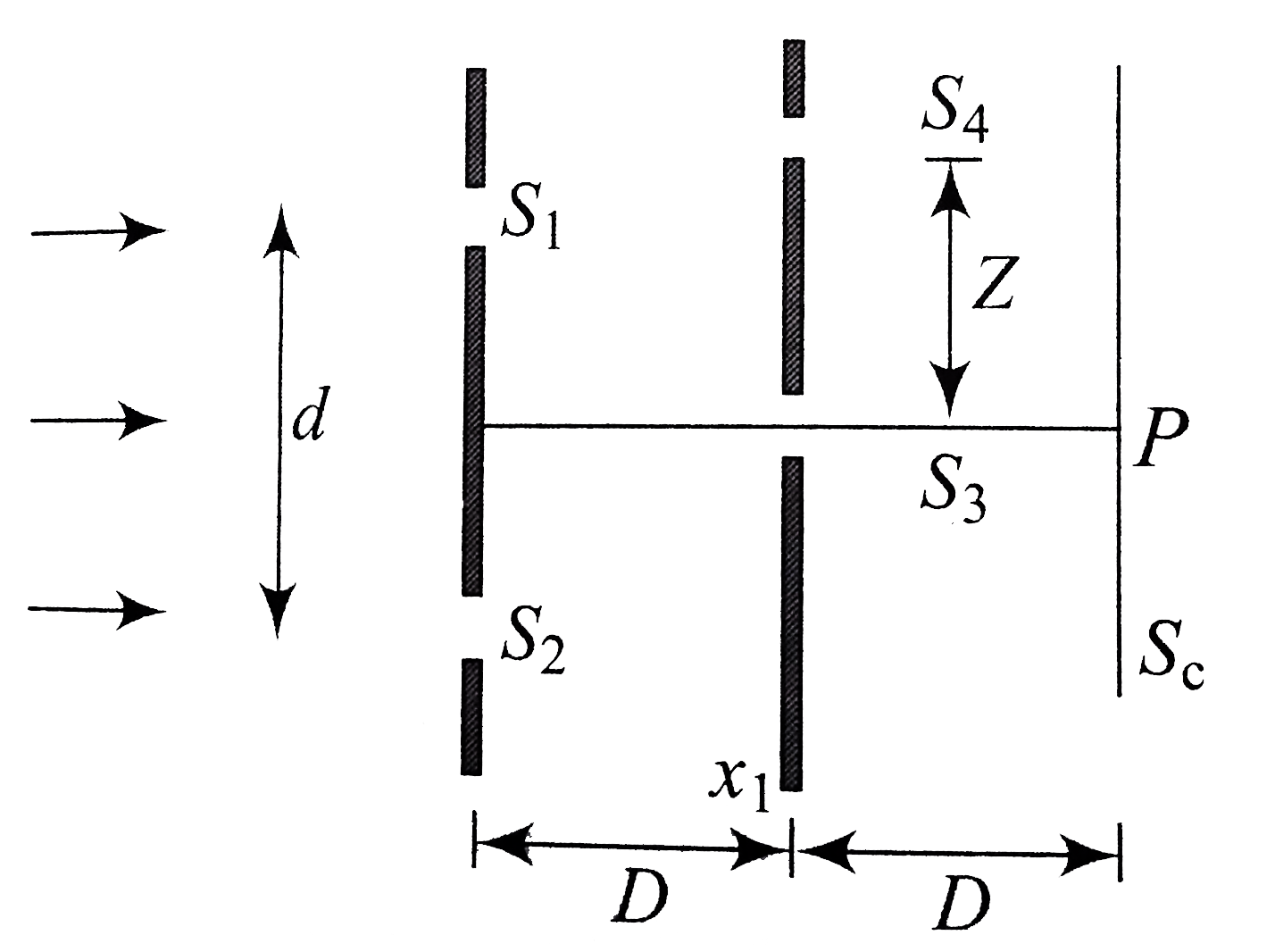
If z=λD4dView SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
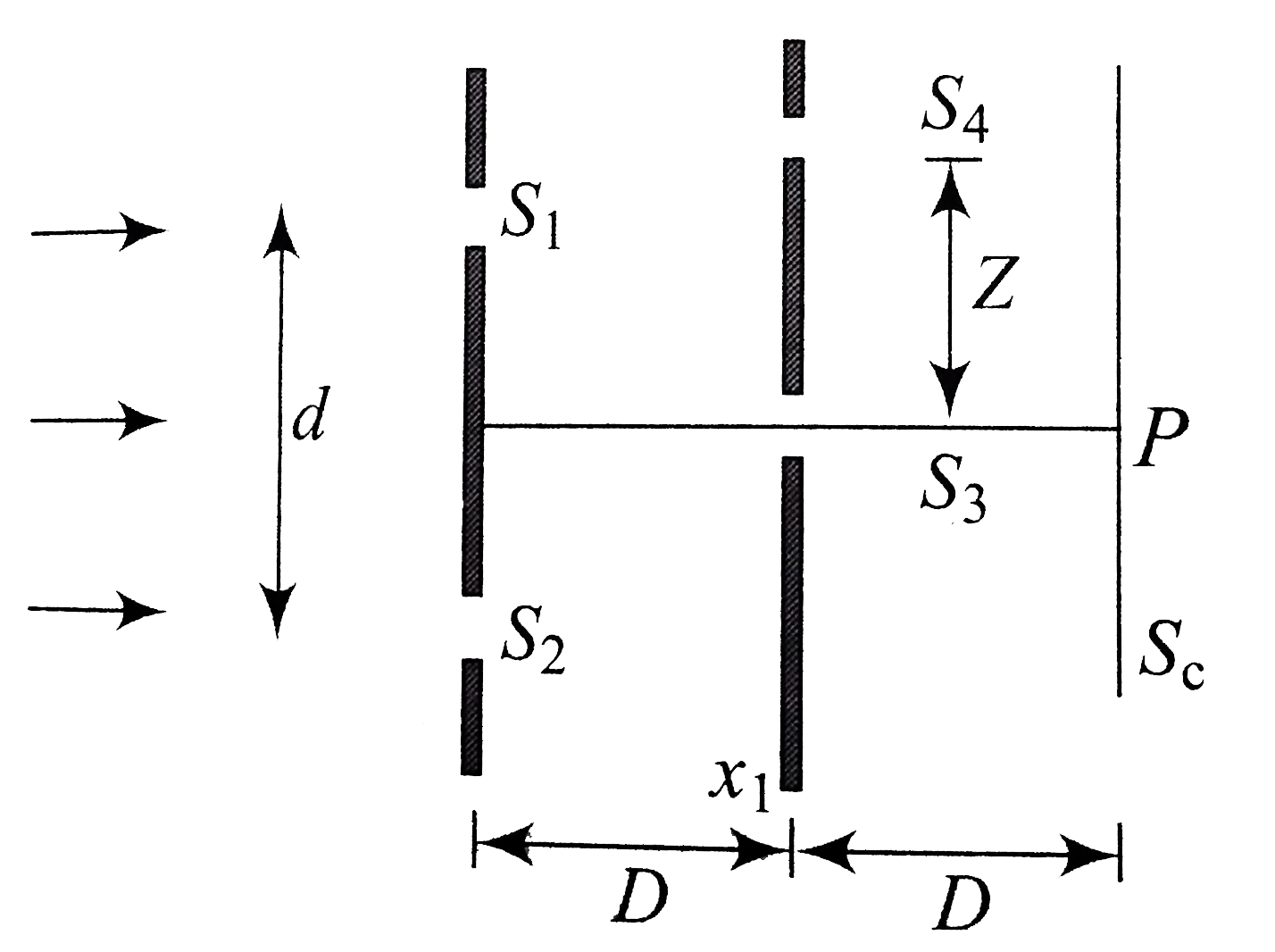
If z=λDdView SolutionTwo parallel slits 0.6mm apart are illuminated by light source of wavelength 6000Å. The distance between two consecutive dark fringe on a screen 1m away from the slits is
View Solution

