When temperature of a material increases, its Young's modulus
increases
decreases
remains same
becomes infinity
The correct Answer is:B
Step by step video, text & image solution for When temperature of a material increases, its Young's modulus by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Level-v(Single answer)
Explore 23 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Multiple answer
Explore 6 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
- MAGNETISMBook:NARAYNAChapter:MAGNETISMExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
When temperature of a ferromagnetic material is increased by 10%, what is the percentage change in its magnetic susceptibility?
View SolutionA thin ring of radius R is made of a material of density ρand Young's modulus Y. If the ring is rotated about its centre in its own plane with angular velocity omega , find the small increases in its radius.
View Solution
Knowledge Check
Young's modulus is
Athe ratio of linear strain to normal stressBthe ratio of normal stress to strainCproduct of linear and normal stressDsquare of the ratio of normal stress to linear strainIf the density of the material increase, the value of young's modulus
AincreasesBdecreasesCfirst increases, then decreasesDfirst decreases, then increasesThe temperature of a wire is doubled. The Young's modulus of elasticity
Awill also doubleBwill becomes four timesCwill remain sameDwill decreases
In the given figure, if the dimensions of the two wires are same but materials are different, then Young's modulus is Extension
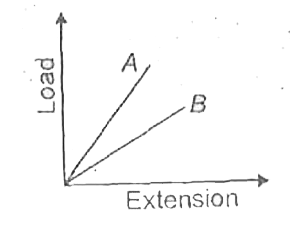
View SolutionThe temperature of a wire is doubled. The young's modulus of elasticity
View SolutionAs temperture increases the Young's modulus of the material of a wire
View SolutionIn the given Fig. 7(CF).2, if the dimensions of the two wires are the same and materials are different, Young's modulus is
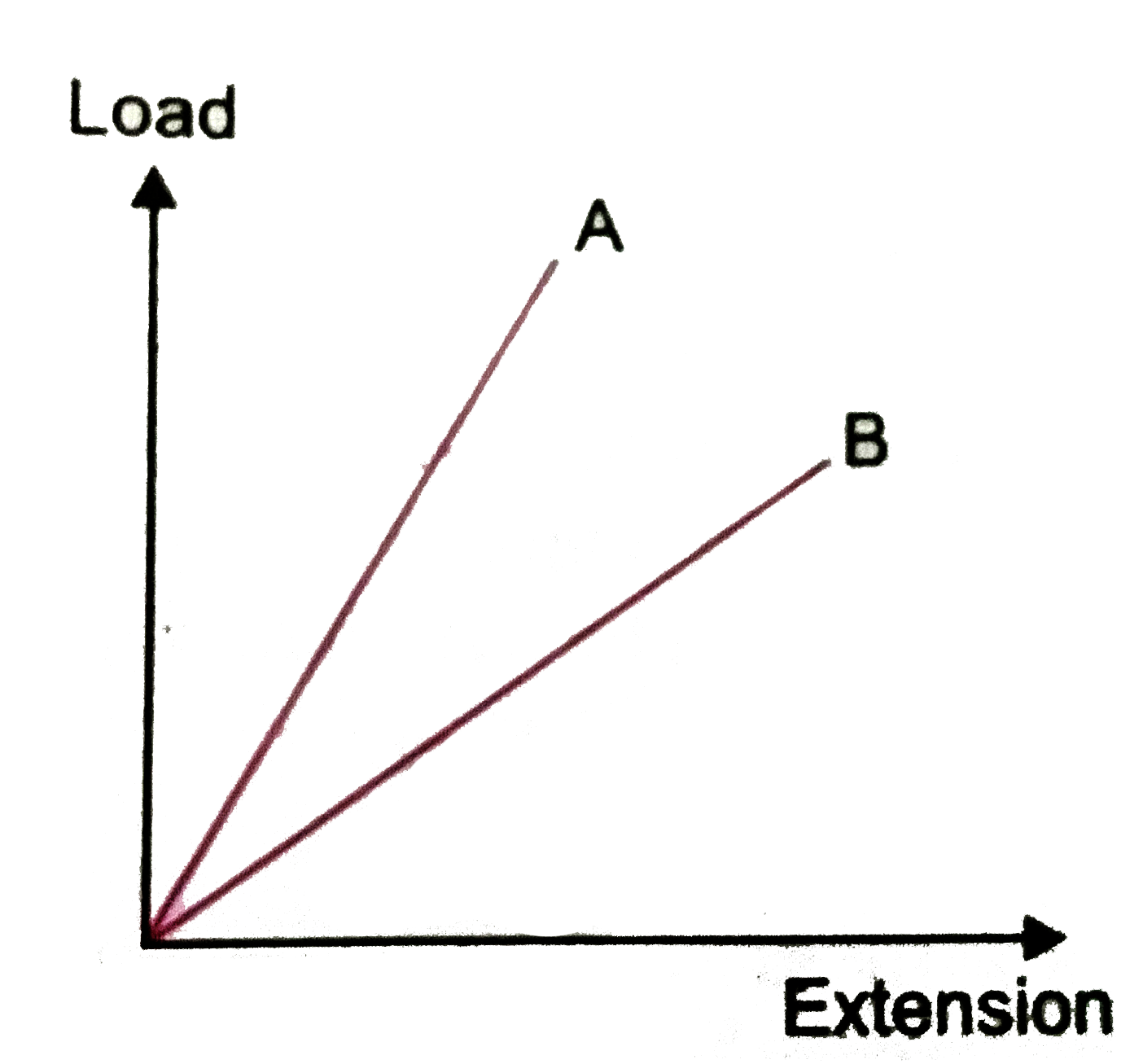
View SolutionWith a rise of temperature, the Young’s modulus :
View Solution

