A steel ring of radius r and cross section area A is fitted on to a wooden disc of radius R(R>r). If Young's modulus be R, then the force with which the steel ring is expanded is
AYRr
AY(R−r)r
YA[R−rr]
YrAR
The correct Answer is:B
Y=T(2πr)A(2π)(R−r)
Topper's Solved these Questions
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Level-v(Single answer)
23 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Multiple answer
6 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
- MAGNETISMBOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
A metal ring of initial radius r and cross-sectional area A is fitted onto a wooden disc of radius R > r. If Youngs modules of metal is Y then tension in the ring is
View SolutionA steel ring is to be fitted on a wooden disc of radius R and thickness d. The inner radius of the ring is r which is slightly smaller than R. The outer radius of the ring is r + b and its thickness is d (same as the disc). There is no change in value of b and d after the ring is fitted over the disc, only the inner radius becomes R. If the Young’s modulus of steel is Y, calculate the longitudinal stress developed in it. Also calculate the tension force developed in the ring.
[Take b<<r]
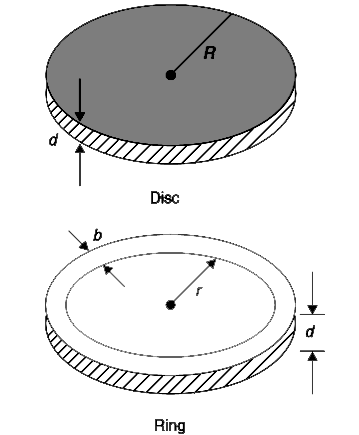
View Solution
Knowledge Check
A metal ring of initial radius r and cross-sectional area A is fitted onto a wooden disc of radius R > r. If Youngs modules of metal is Y then tension in the ring is
AAYRrBAY(R−r)rCYA(R−rr)DYrARA metallic rod of radius 2cm and cross sectional area 4cm2 is fitted into a wooden circular disc of radisu 4cm. If the Young's modulus of the materail of the ring is 2×1011N/m2, the force with which the metal ring expands is:
A2×107NB8×107NC4×107ND6×107NA steel wire is stretched by 5kwt. If the radius of the wire is doubled its Young's modulus
Aremains unchangedBbecomes doubleCbecomes halfDbecomes 1/4 times
A uniform ring of radius R and made up of a wire of cross - sectional radius r is rotated about its axis with a frequency f. If density of the wire is ρ and young's modulus is Y . Find the fractional change in radius of the ring .
View SolutionA ring of radius R is made of a thin wire of material of density ρ, having cross-section area a and Young's modulus y. The ring rotates about an axis perpendicular to its plane and through its centre. Angular frequency of rotation is ω.
The tension in the ring will be
View SolutionA ring of radius R is made of a thin wire of material of density ρ, having cross-section area a and Young's modulus y. The ring rotates about an axis perpendicular to its plane and through its centre. Angular frequency of rotation is ω.
The ratio of kinetic energy to potential energy is
View SolutionTwo wire of same radius and lengh the are subjected to the same load. One wire is of steel and the other is of copper. If the Young's modulus of steel is twice that of copper, the ratio the energy stored per unit volume in steel to that of copper wire is
View SolutionA steel wire of length 5 m and area of cross-section 4mm2 is stretched by 2 mm by the application of a force. If young's modulus of steel is 2×1011N/m2, then the energy stored in the wire is
View Solution
