An ACrms voltage of 2V having a frequency of 50KHz is applied to a condenser of capacity of 10μF. The maximum value of the magnetic field between the plates of the condenser if the radius of plate is 10cm is
0.4pμ
4πμT
2μT
40πμT
The correct Answer is:C
To find the maximum value of the magnetic field between the plates of a capacitor when an AC rms voltage is applied, we can follow these steps:
Step 1: Convert Given Values
- Given:
- AC rms voltage, Vrms=2V
- Frequency, f=50kHz=50×103Hz
- Capacitance, C=10μF=10×10−6F
- Radius of the plates, r=10cm=0.1m
Step 2: Calculate Maximum Voltage
The maximum voltage Vmax can be calculated from the rms voltage using the formula:
Vmax=Vrms×√2
Substituting the values:
Vmax=2×√2≈2.828V
Step 3: Calculate Current
The current I through the capacitor can be calculated using the formula:
I=CdVdt
For an AC voltage, dV/dt can be expressed as:
dVdt=2πfVmax
Substituting the values:
dVdt=2π(50×103)(2.828)≈628318.53V/s
Now, substituting back to find I:
I=C⋅dVdt=(10×10−6)⋅(628318.53)≈6.283A
Step 4: Calculate Magnetic Field
The magnetic field B between the plates of the capacitor can be calculated using the formula:
B=μ0I2πr
Where μ0=4π×10−7T⋅m/A. Substituting the values:
B=(4π×10−7)(6.283)2π(0.1)
This simplifies to:
B=(4×10−7)(6.283)0.2=2.513×10−60.2≈1.2565×10−5T
Step 5: Convert to Microtesla
To convert the magnetic field from Tesla to microtesla:
B≈12.565μT
Final Answer
The maximum value of the magnetic field between the plates of the capacitor is approximately 12.57μT.
---
- Given:
- AC rms voltage, Vrms=2V
- Frequency, f=50kHz=50×103Hz
- Capacitance, C=10μF=10×10−6F
- Radius of the plates, r=10cm=0.1m
The maximum voltage Vmax can be calculated from the rms voltage using the formula:
Vmax=Vrms×√2
Substituting the values:
Vmax=2×√2≈2.828V
The current I through the capacitor can be calculated using the formula:
I=CdVdt
For an AC voltage, dV/dt can be expressed as:
dVdt=2πfVmax
Substituting the values:
dVdt=2π(50×103)(2.828)≈628318.53V/s
Now, substituting back to find I:
I=C⋅dVdt=(10×10−6)⋅(628318.53)≈6.283A
The magnetic field B between the plates of the capacitor can be calculated using the formula:
B=μ0I2πr
Where μ0=4π×10−7T⋅m/A. Substituting the values:
B=(4π×10−7)(6.283)2π(0.1)
This simplifies to:
B=(4×10−7)(6.283)0.2=2.513×10−60.2≈1.2565×10−5T
To convert the magnetic field from Tesla to microtesla:
B≈12.565μT
The maximum value of the magnetic field between the plates of the capacitor is approximately 12.57μT.
Topper's Solved these Questions
- ELECTRO MAGNETIC WAVESBook:NARAYNAChapter:ELECTRO MAGNETIC WAVESExercise:LEVEL- III
Explore 10 Videos
- ELECTRO MAGNETIC WAVESBook:NARAYNAChapter:ELECTRO MAGNETIC WAVESExercise:NCERT based
Explore 8 Videos
- ELECTRO MAGNETIC WAVESBook:NARAYNAChapter:ELECTRO MAGNETIC WAVESExercise:LEVEL -I(C.W.)
Explore 21 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Level-II (H.W)
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSERTION & REASON
Explore 6 Videos
Similar Questions
A condenser is charged using a constant current. The ratio of the magnetic field at a distance of R2 and R from the axis of condenser (R is the radius of plate) while charging is
View SolutionThere are 10 condensers each of capacity 5μF. The ratio between maximum and minimum capacity obtained from these condensers will be
View Solution
Knowledge Check
A parallel plate air condenser of capacity 10μF is charged to a potential of 1000V. The energy of the condenser is
A5 JB4 JC2.5 JD10 JAn AC source having a frequency of 50Hz and voltage supply of 300v is applied directly to the condenser of capacity 100μF. The peak and rms values of displacement current are
A9.42A, 9.42√2AB9.42√2A, 9.42√2AC9.42√2A, 9.42AD9.42A, 9.42AA parallel plate air condenser of capacity 4μF is charged to a potential of 1000 V. the energy of the condenser is
A1 jouleB4 jouleC6 jouleD2 joule
A condenser of capacity 50pF is connected to an AC supply of 220V50Hz. The rms value of magnetic field at a distance of 5cm from the axis is
View SolutionA parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is
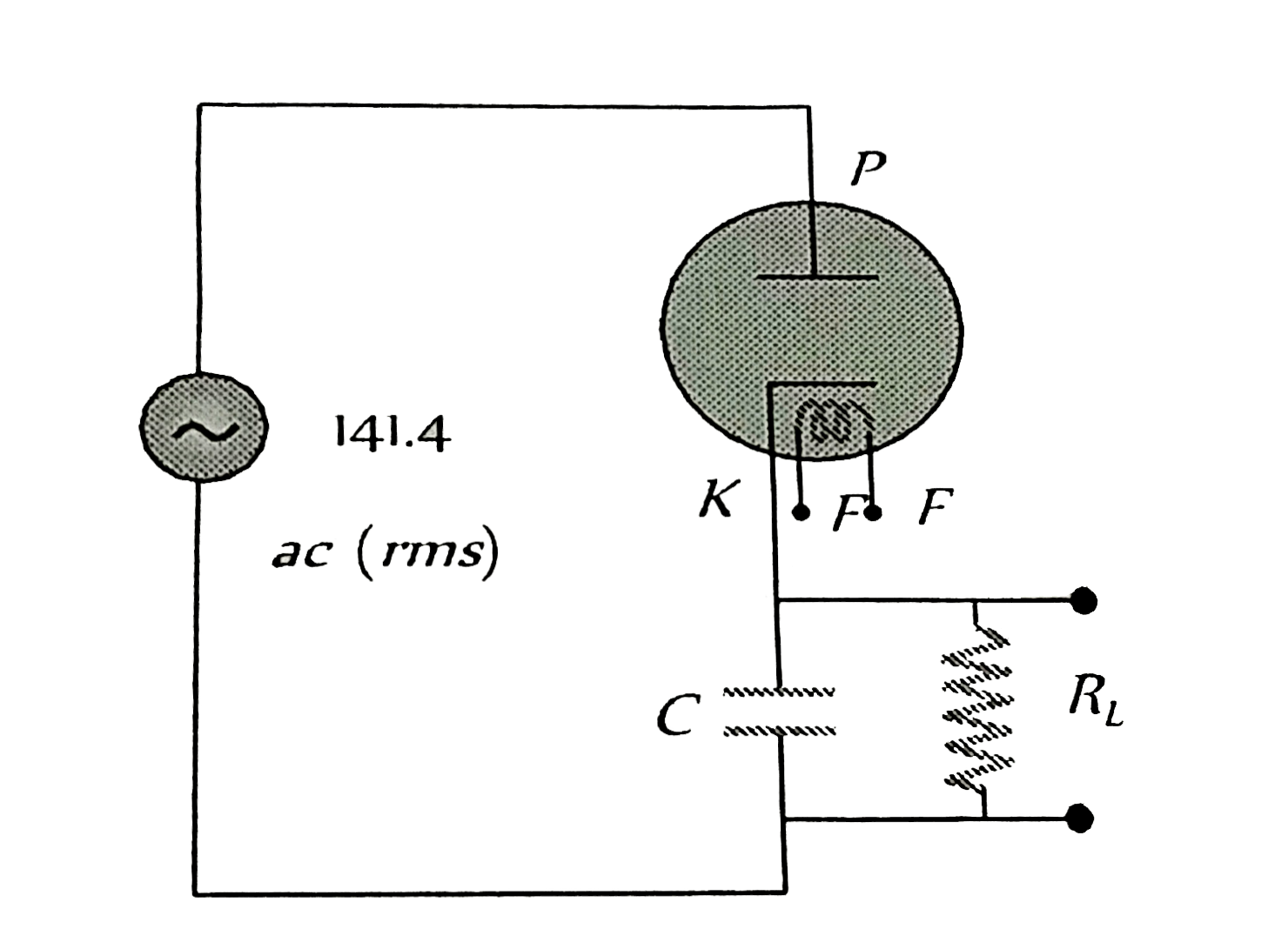
View SolutionAn alternating voltage of 141.4V(rms) is applied to a vacuum diode as shown in the figure. The maximum potential difference across the condenser will be
View SolutionA condenser has a capacity of 2μF and is cahrged to a potential of 50 V. the energy stored in it is
View SolutionThe capacity of a paralel plate condenser is 12μF. What is its new capacity if the separation between the plates is doubled and the area is halved?
View Solution

