निम्नलिखित कथनों पर विचार कीजिए
1 . रेखाओं y=mx+c1 और y=mx+c2 के बीच की दूरी |c1+c2|√1+m2 है ।
2. रेखाओं ax+by+c1=0 और ax+by+c2=0 के बीच की दूरी |c1+c2|√a2+b2 है ।
3. रेखाओं x=c1 और x=c2 के बीच की दूरी |c1−c2| है
उपरोक्त कथनों में से कोन -से सही है ?
1 और 3
2 और 3
1 और 3
1,2 और3
कथन 1
दी गई रेखाएँ ,
y=mx+c1,
और y=mx+c2
दोनों रेखाएँ समान्तर है ।
अतः दोनों रेखाओं की दूरी =∣∣∣c1−c2√1+m2∣∣∣
कथन 1 सही है ।
कथन 2
दी गई रेखाएँ ax+by+c1=0
और ax+by+c2=0
दोनों रेखाएँ समान्तर है ।
∴ दोनों रेखाओं की बीच की दूरी =∣∣∣c1−c2√a2+b2∣∣∣
कथन 3
दी गई रेखाएँ, x=C1 तथा x=C2 दोनों रेखाएँ समान्तर है ।
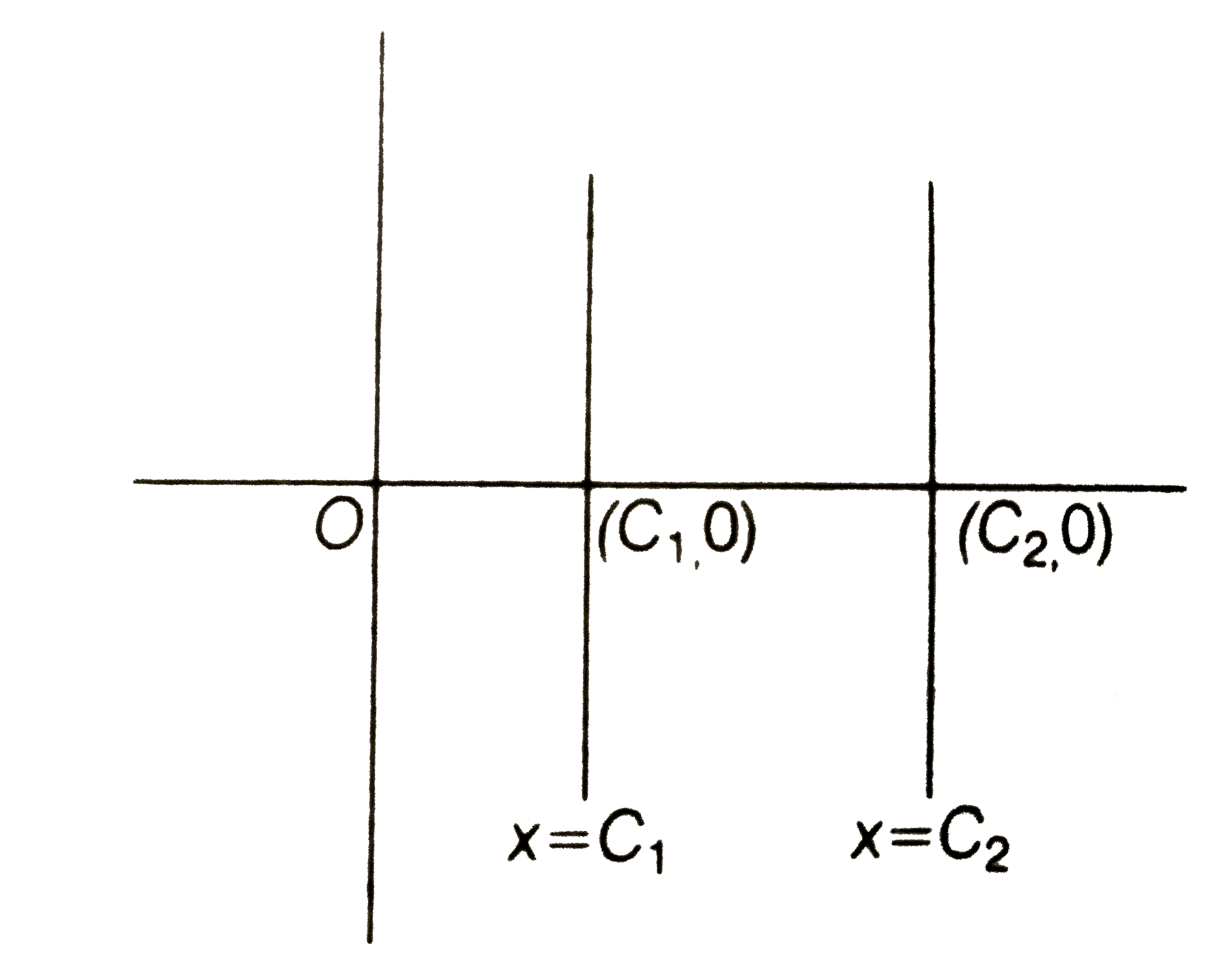
∴ दोनों रेखाओं के बीच की दूरी : |C1−C2|
Topper's Solved these Questions
Similar Questions
यदि n∈N है, तो 121n−25n+1900n−(−4)n निम्नलिखित में से किससे विभाज्य है ?
View Solutionअनुक्रम 25,−125,625,−3125,... का n वां पद क्या है ?
View SolutionProve that (C_(0)+C_(1))(C_(1)+C_(2))(C_(2)+C_(3))(C_(n-1)+C_(n))=((n+1)^(n))/(n!)*c_(0)*C_(1)*C_(2).........
View SolutionIf (1+x+x^(2))^(n)=(C_(0)+C_(1)x+C_(2)x^(2)+.........) then the value of C_(0)C_(1)-C_(1)C_(2)+C_(2)C_(3)...
View SolutionConsider the following statements :
1. The distance between the lines
y=mx+c1 and y=mx+c2 is |c1−c2|√1−m2.
2. The distance between the lines ax+by+c1 and ax+by+c2=0 is |c1−c2|√a2+b2.
3. The distance between the lines x=c and x=c2 is |c1−c2|. Which of the above statements are correct ?
View SolutionEvaluate ∣∣ ∣∣.xC1.xC2.xC3.yC1.yC2.yC3.xC1.zC2.zC3∣∣ ∣∣
View SolutionIf (1+x)n=C0+C1x+C2x2+C3x3+…+Cnxn, then
C0−(C0−C1)+(C0+C1+C2)−(C0+C1+C2+C3)+...+(−1)n−1
(C0)+C1+C2+...+Cn−1) , when n is even integer is
View SolutionTan−1c1x−yc1y+x+Tan−1c2−c11+c2c1+Tan−1c3−c21+c3c2+...Tan−11cn=
View SolutionIf (1+x)n=C0+C1x+C2x2+.....+Cnxn then show :
C0.Cn+C1.Cn−1+C2.Cn−2+....+Cn.C0=(2n)!(n!)2
View SolutionIf (1+x)n=C0+C1x+C2x2+.....+Cnxn then show :
C0C1+C1C2+C2C3+.....+C_(n−1)Cn=(2n)!(n+1)!(n−1)!
View SolutionIf (1+x+x2)n=c0+c1x+c2x2+…., then the value of c0c1−c1c2+c2c3−…… is
View Solutionयदि (1+x)n=C0+C1x+C2x2+....+Cnxn तब C0−(C0+C1)+(C0+C1+C2)−(C0+C1+C2+C3) जहाँ n रागपूर्णांक है
View SolutionEvaluate ∣∣ ∣∣.xC1.xC2.xC3.yC1.yC2.yC3.xC1.zC2.zC3∣∣ ∣∣
View SolutionTan−1(c1x−yc1y+x)+Tan−1(c2−c11+c2c1)+Tan−1(c3−c21+c3c2)+…+Tan−1(1cn)=
View SolutionIf (1+x)n= C0+C1.x+C2.x2+..+Cn.xn then C0+2.C1+3.C2+..+(n+1).Cn=
View Solution

