Relation between Y,ηandKis
Y3=3K+1η
9Y=η3+1K
3Y=1η+13K
Y3=3η+1K
The correct Answer is:C
To find the relation between Young's modulus (Y), modulus of rigidity (η), and bulk modulus (K), we can use the known formulas for these moduli in terms of Poisson's ratio (μ).
1. Identify the Definitions:
- Young's Modulus (Y): It measures the ability of a material to withstand changes in length when under lengthwise tension or compression.
- Modulus of Rigidity (η): It measures the material's response to shear stress (the ratio of shear stress to shear strain).
- Bulk Modulus (K): It measures a substance's response to uniform pressure applied in all directions.
2. Use the Relationship Formulas:
- The relationship between Young's modulus (Y), modulus of rigidity (η), and Poisson's ratio (μ) is given by:
Y=2η(1+μ)
- The relationship between Young's modulus (Y), bulk modulus (K), and Poisson's ratio (μ) is given by:
Y=3K(1−2μ)
3. Set Up the Equations:
- From the first equation, we can express μ in terms of Y and η:
μ=Y2η−1
- From the second equation, we can express μ in terms of Y and K:
μ=3K−Y2Y
4. Equate the Two Expressions for μ:
- Set the two expressions for μ equal to each other:
Y2η−1=3K−Y2Y
5. Cross Multiply and Simplify:
- Cross-multiplying gives:
2Y(Y2η−1)=3K−Y
- This simplifies to:
Y2η−2Y=3K−Y
- Rearranging gives:
Y2η+Y−3K=2Y
6. Final Relation:
- Rearranging the equation leads to:
Y2η=3K−Y
- This can be further manipulated to find a relation between Y, η, and K.
7. Conclusion:
- The final relation can be expressed as:
1Y=13K+1η
- Young's Modulus (Y): It measures the ability of a material to withstand changes in length when under lengthwise tension or compression.
- Modulus of Rigidity (η): It measures the material's response to shear stress (the ratio of shear stress to shear strain).
- Bulk Modulus (K): It measures a substance's response to uniform pressure applied in all directions.
- The relationship between Young's modulus (Y), modulus of rigidity (η), and Poisson's ratio (μ) is given by:
Y=2η(1+μ)
- The relationship between Young's modulus (Y), bulk modulus (K), and Poisson's ratio (μ) is given by:
Y=3K(1−2μ)
- From the first equation, we can express μ in terms of Y and η:
μ=Y2η−1
- From the second equation, we can express μ in terms of Y and K:
μ=3K−Y2Y
- Set the two expressions for μ equal to each other:
Y2η−1=3K−Y2Y
- Cross-multiplying gives:
2Y(Y2η−1)=3K−Y
- This simplifies to:
Y2η−2Y=3K−Y
- Rearranging gives:
Y2η+Y−3K=2Y
- Rearranging the equation leads to:
Y2η=3K−Y
- This can be further manipulated to find a relation between Y, η, and K.
- The final relation can be expressed as:
1Y=13K+1η
Topper's Solved these Questions
- ELASTICITYBook:TARGET PUBLICATIONChapter:ELASTICITYExercise:Evaluation test
Explore 14 Videos
- ELASTICITYBook:TARGET PUBLICATIONChapter:ELASTICITYExercise:Critical Thinking
Explore 54 Videos
- CURRENT ELECTRICITY Book:TARGET PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:Evaluation Test
Explore 6 Videos
- ELECTROMAGNETIC INDUCTIONBook:TARGET PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EVALUATION TEST
Explore 8 Videos
Similar Questions
Knowledge Check
The relation between Y. η and B is
A1Y=13η+19BB9Y=1η+3BC1η=1B+1YD9Y=3η+1BThe relation between ΔU is :
AΔH=ΔU+RTBΔH=ΔU−ΔgnRTCΔH=ΔU+ΔgnRTDΔU=ΔH+ΔgnRT
Relation between (X) and (Y) is :AwnantiomersBdiastereomersCE and Z isomerDconstitutional isomer
If x% of y is 150 and y% of z is 300, then the relation between x and z is :
यदि y का x% 150 है और z का y% 300 है, तो x और z में क्या संबंध है ?
View SolutionRelation between A and 2A is
View SolutionRelation between (A) and (B) is :
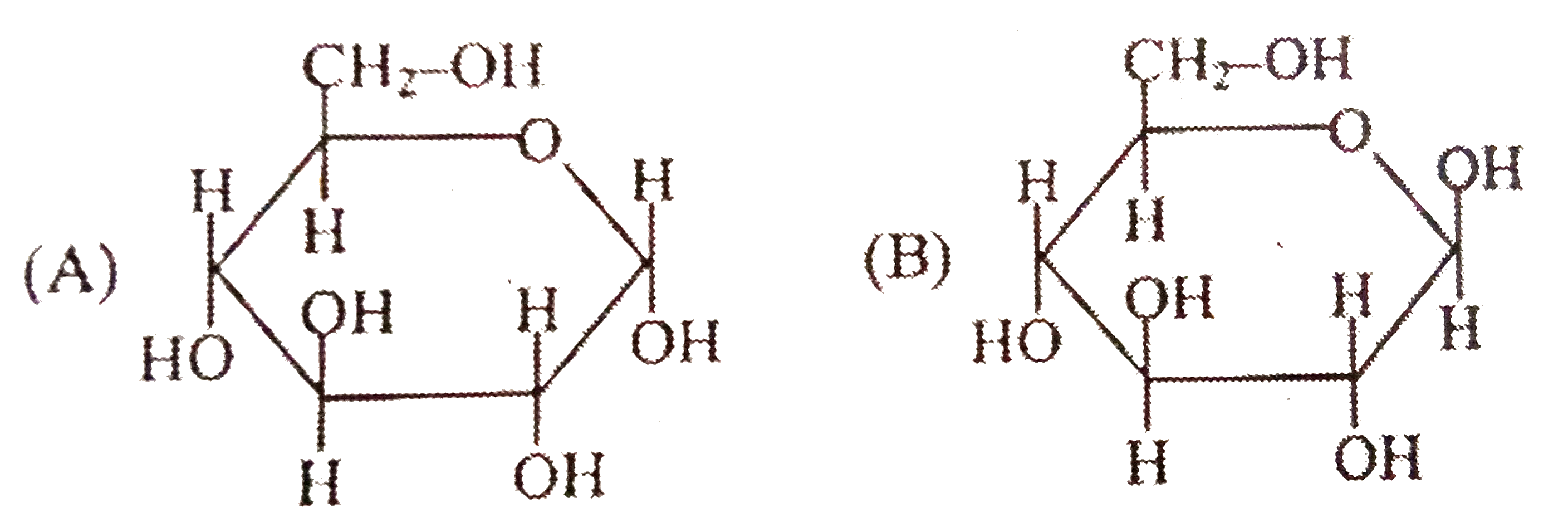
View SolutionRelation between (A) and (B) is
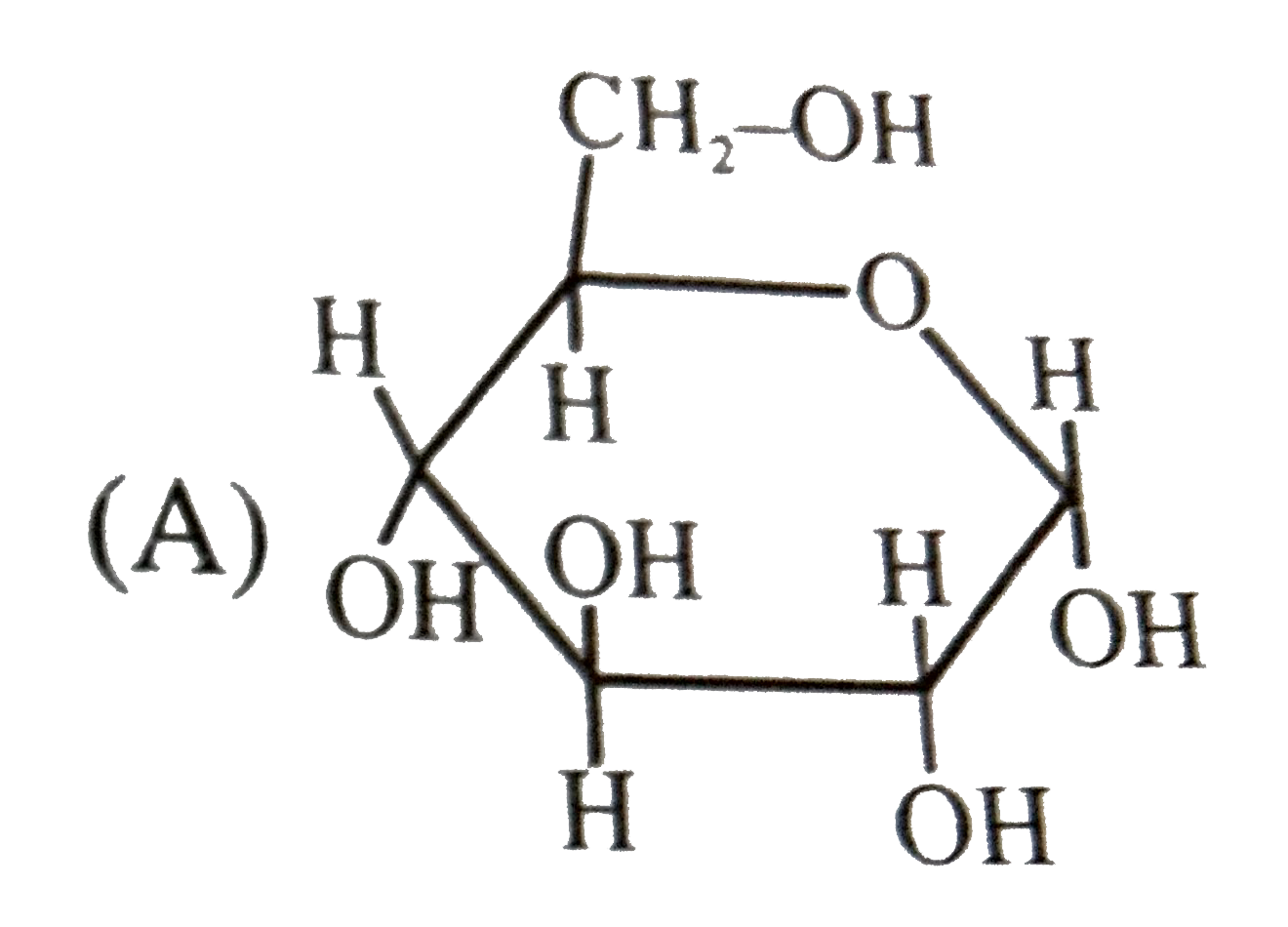
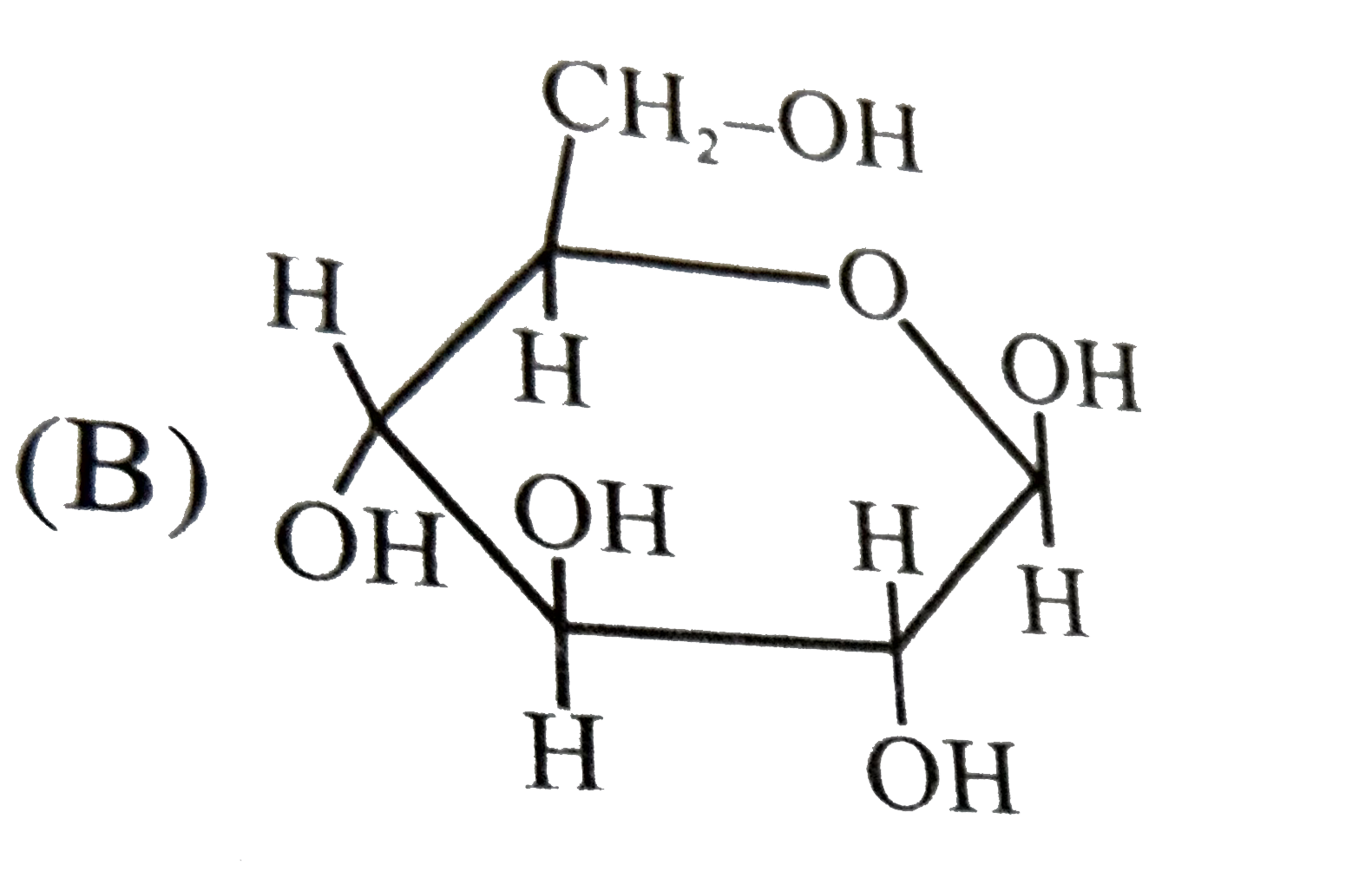
View Solution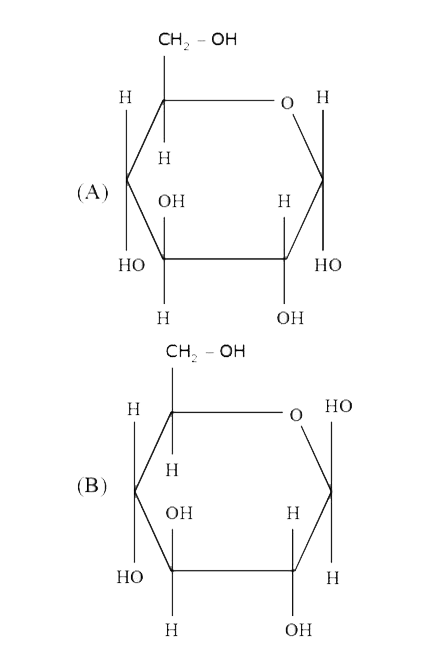
Relation between (A) and (B) is
View Solution

