The tangential velocity of a particle making p rotations along a circle of radius π in t seconds is
2πpt2
2πp2t
π2p2t
2π2pt
The correct Answer is:D
To find the tangential velocity of a particle making P rotations along a circle of radius π in t seconds, we can follow these steps:
1. Identify the Given Values:
- Radius R=π
- Number of rotations P
- Time t seconds
2. Understand the Relationship Between Linear and Angular Velocity:
- The tangential velocity V is related to angular velocity ω by the formula:
V=R⋅ω
3. Calculate Angular Velocity ω:
- Angular velocity ω is defined as the number of radians rotated per second.
- Each rotation corresponds to 2π radians. Therefore, for P rotations, the total radians is:
Total radians=P⋅2π
- To find the angular velocity, we divide the total radians by the time t:
ω=P⋅2πt
4. Substitute ω into the Tangential Velocity Formula:
- Now substitute ω back into the equation for V:
V=R⋅ω=π⋅(P⋅2πt)
5. Simplify the Expression:
- Simplifying the above expression gives:
V=2π2Pt
6. Final Result:
- Therefore, the tangential velocity V of the particle is:
V=2π2Pt
Conclusion:
The tangential velocity of the particle making P rotations along a circle of radius π in t seconds is 2π2Pt.
- Radius R=π
- Number of rotations P
- Time t seconds
- The tangential velocity V is related to angular velocity ω by the formula:
V=R⋅ω
- Angular velocity ω is defined as the number of radians rotated per second.
- Each rotation corresponds to 2π radians. Therefore, for P rotations, the total radians is:
Total radians=P⋅2π
- To find the angular velocity, we divide the total radians by the time t:
ω=P⋅2πt
- Now substitute ω back into the equation for V:
V=R⋅ω=π⋅(P⋅2πt)
- Simplifying the above expression gives:
V=2π2Pt
- Therefore, the tangential velocity V of the particle is:
V=2π2Pt
The tangential velocity of the particle making P rotations along a circle of radius π in t seconds is 2π2Pt.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:TARGET PUBLICATIONChapter:CIRCULAR MOTIONExercise:EVALUATION TEST
Explore 11 Videos
- CIRCULAR MOTIONBook:TARGET PUBLICATIONChapter:CIRCULAR MOTIONExercise:CRITICAL THINKING
Explore 93 Videos
- ATOMS, MOLECULES AND NUCLEI Book:TARGET PUBLICATIONChapter:ATOMS, MOLECULES AND NUCLEI Exercise:Evaluation test
Explore 19 Videos
- CURRENT ELECTRICITY Book:TARGET PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:Evaluation Test
Explore 6 Videos
Similar Questions
Figure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5 m at a given instant of time. At this instant, Find: (i) the radial acceleration, (ii) the speed of the particle and (iii) its tangential acceleration.
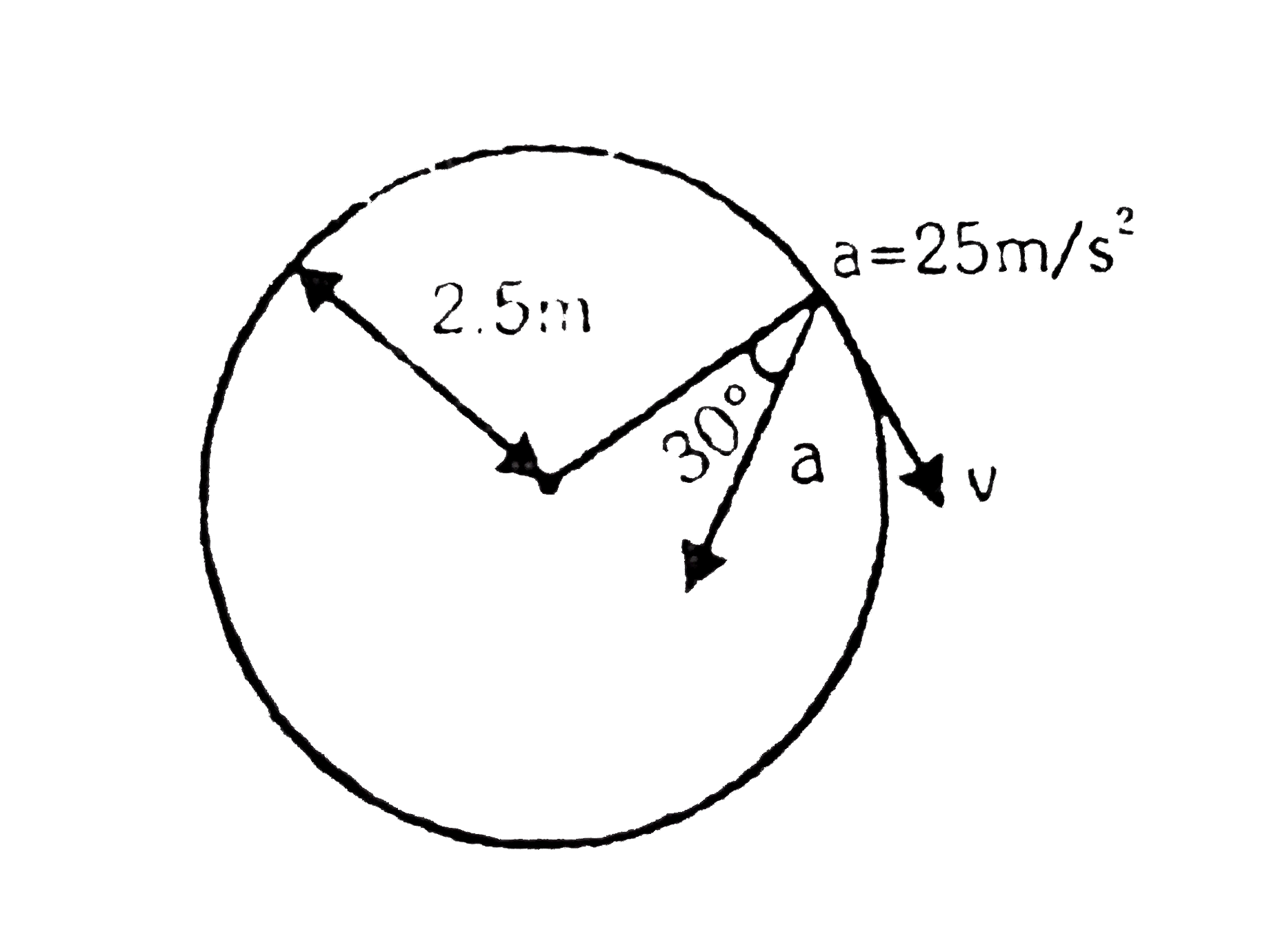
View SolutionFigur shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5m at a given instant of time. At this instant, find:
(a) the radius acceleration,
(b) the speed of the acceleration,
(c) its tangential acceleration.

View Solution
Knowledge Check
The angular velocity of a particle moving in a circle of radius 50cm is increased in 5 min from 100 revolutions per minute to 400 revolutions per minute. Find the tangential acceleration of the particle.
A60ms−2Bπ/30ms−2Cπ/15ms−2Dπ/60ms−2The distance of a particle moving on a circle of radius 12 m measured from a fixed point on the circle and measured along the circle is given by s=2t3 (in meters). The ratio of its tangential to centripetal acceleration at t = 2s is
A1:1B1:2C2:1D3:1A particle at t=0 second is at point A and moves along the shown path (ABCDF) with uniform speed v=(1+π3)m/s. Both the straight segments AB and DE are along the diameter BD of semicircle BCD radius R=1 meter. Find the instant of time at which the instantaneous velocity of the particle is along the direction of average velocity from t=0 second to that instant.
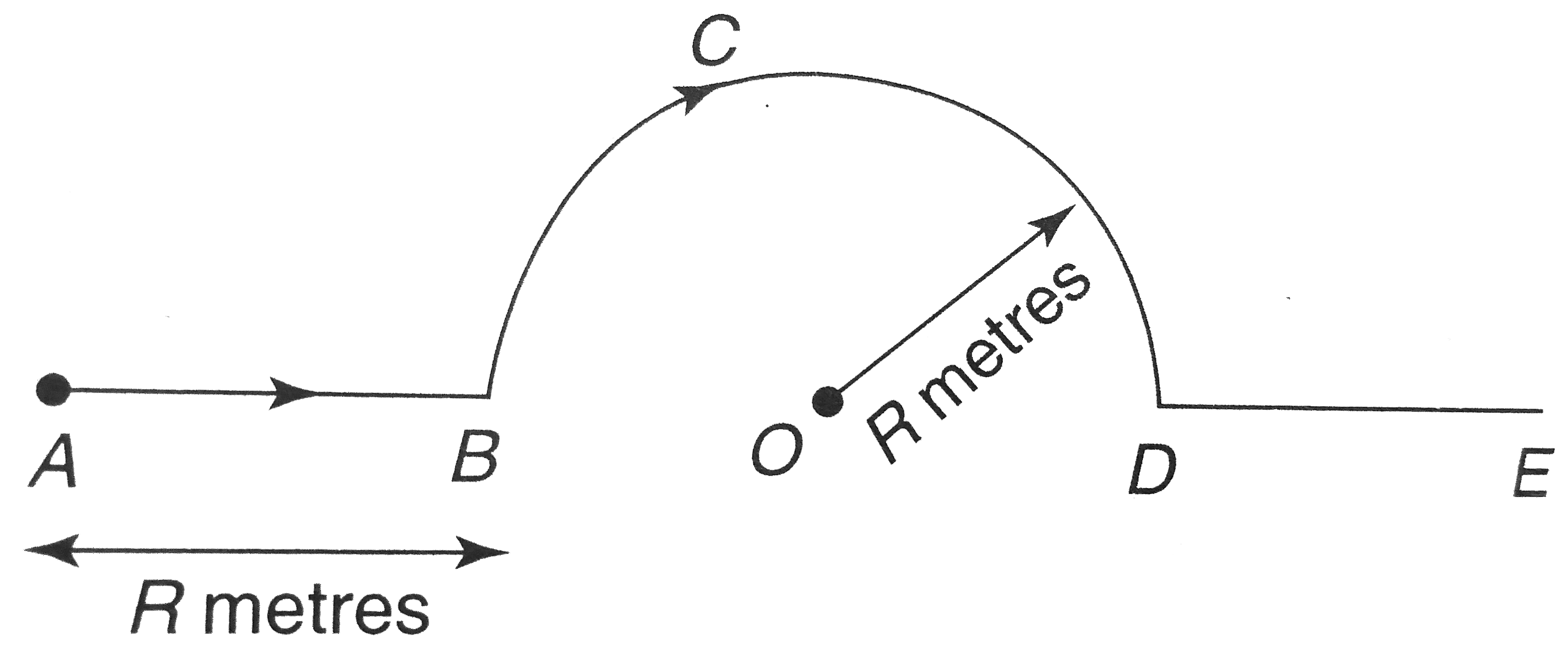 A2 secB4 secC1 secD1.5 sec
A2 secB4 secC1 secD1.5 sec
Tangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
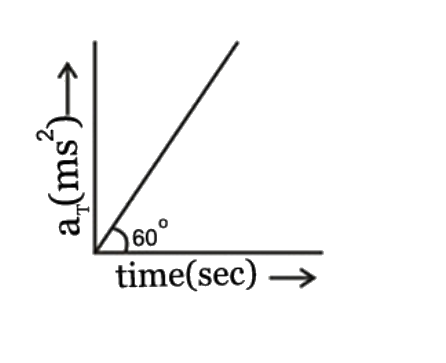
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance S as K=βS2 , where β is a constant. Tangential acceleration of the particle is proportional to
View SolutionWhat will be sign of the velocity of the point P′, which is the projection of the velocity of the reference particle P? P is moving in the circle of radius R in anticlockwise direction.

View SolutionIn figure, what be the sign of the velocity of the point P', which is the projection of the velocity of the reference particle P.P is moving in a circle of radius R in anti-clockwise direction.

View SolutionA particle is revolving in a circle of radius 1 m with an angular speed of 12 rad/s. At t = 0, it was subjected to a constant angular acceleration α and its angular speed increased to (480π) rotation per minute (rpm) in 2 sec. Particle then continues to move with attained speed. Calculate
(i) angular acceleration of the particle,
(ii) tangential velocity of the particle as a function of time.
(iii) acceleration of the particle at t = 0.5 second and at t = 3 second
(iv) angular displacement at t = 3 second.
View Solution

