A proton is moving perpendicular to a uniform magnetic field of 2.5 tesla with 2 MeV kinetic energy. The force on proton is _______N. (Mass of proton= 1.6×10−27 kg, charge of proton =1.6×10−19 C)
8×10−12
8×10−11
3×10−11
3×10−10
The correct Answer is:A
To find the force on a proton moving perpendicular to a magnetic field, we can use the formula for magnetic force:
F=q⋅v⋅B⋅sin(θ)
Where:
- F is the magnetic force,
- q is the charge of the proton,
- v is the velocity of the proton,
- B is the magnetic field strength,
- θ is the angle between the velocity and the magnetic field.
Step 1: Convert the kinetic energy of the proton to velocity
The kinetic energy (KE) of the proton is given as 2 MeV. We need to convert this to joules:
1 MeV = 1.6×10−13 Joules
Thus,
KE=2MeV=2×1.6×10−13J=3.2×10−13J
Using the kinetic energy formula:
KE=12mv2
We can rearrange this to solve for v:
v=√2⋅KEm
Substituting the values:
- Mass of the proton, m=1.6×10−27kg
- Kinetic energy, KE=3.2×10−13J
v=√2⋅3.2×10−131.6×10−27
Calculating this:
v=√6.4×10−131.6×10−27=√4×1014=2×107m/s
Step 2: Calculate the force using the magnetic force formula
Now that we have the velocity, we can calculate the magnetic force.
Given:
- Charge of the proton, q=1.6×10−19C
- Magnetic field strength, B=2.5T
- Velocity, v=2×107m/s
- Since the proton is moving perpendicular to the magnetic field, sin(90∘)=1.
Now substituting these values into the force formula:
F=q⋅v⋅B
F=(1.6×10−19)⋅(2×107)⋅(2.5)
Calculating this:
F=1.6×2×2.5×10−19×107
F=8×10−12N
Final Answer:
The force on the proton is 8×10−12N.
---
- F is the magnetic force,
- q is the charge of the proton,
- v is the velocity of the proton,
- B is the magnetic field strength,
- θ is the angle between the velocity and the magnetic field.
The kinetic energy (KE) of the proton is given as 2 MeV. We need to convert this to joules:
- Kinetic energy, KE=3.2×10−13J
Now that we have the velocity, we can calculate the magnetic force.
- Charge of the proton, q=1.6×10−19C
- Magnetic field strength, B=2.5T
- Velocity, v=2×107m/s
- Since the proton is moving perpendicular to the magnetic field, sin(90∘)=1.
The force on the proton is 8×10−12N.
Topper's Solved these Questions
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - Evaluation Test
12 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - Critical Thinking Introduction
38 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
- MAGNETISMBOOK - TARGET PUBLICATIONCHAPTER - MAGNETISMEXERCISE - MCQs
150 Videos
Similar Questions
Knowledge Check
A proton of energy 2MeV is moving perpendicular to uniform magnetic field of 2.5T. The form on the proton is (Mp=1.6×10−27Kg and q=e=1.6×10−19C)
A3×10−10 NB8×1011 NC3×10−11 ND8×10−12 NA proton is projected with a velocity 107ms−1, at right angles to a uniform magnetic field of induction 100mT. The time ( in second ) taken by the proton to traverse 90∘ are is :( Mass of proton =1.65×10−27kg an charge of proton =1.6×10−19C)
A0.81×10−7B1.62×10−7C2.43×10−7D3.24×10−7A proton with energy of 2 MeV enters a region of a uniform magnetic field of 2.5 T normally. The magnetic force on the proton is (Take mass of proton to be
A3×10−12NB3×10−8NC8×10−12ND3×10−10N
(a) A proton is moving in a magnetic field. The field ¯¯¯B is into the plane of the page. The velocity vector, ¯v lies in the plane of the page. Perpendicular to ¯¯¯B. Describe the motion of proton.
(b) In part (a) : if the radius fo the circle is 0.5 m and the magnitude of the magnetic field is 1.2 wbm2. find the frequency of revolution and the kinetic energy of the proton. Charge of the proton =1.60×10−19 C. Mass of the proton =1.67×10−27 kg.
View SolutionA beam of protons with a velocity 4×105 m/sec enters a uniform magnetic field of 0.3 Testa at an angle of 60∘ to the magnetic field. Find the radius of the helical path taken by the proton beam. Also find the pitch of the helix, which is the distance travelled by a proton in the beam parallel to the magnetic field during one period of rotation
[Mass of proton =1.67×10−27 kg. charge on proton =1.6×1019C]
View SolutionThe maximum kinetic energy of protons in a cyclotron of radius 0.4 m in a magnetic field of 0.5 T is (mass of proton = 1.67×10−27 kg, charge of proton =1.6×10−19 C)
View SolutionA proton of energy 2MeV is moving perpendicular to uniform magnetic field of 2.5T. The form on the proton is (Mp=1.6×10−27Kg and q=e=1.6×10−19C)
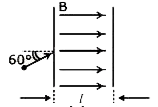
View SolutionThe figure shows a region of length ‘l’ with a uniform magnetic field of 0.3 T in it and a proton entering the region with velocity 4×105 ms−1 making an angle 60∘ with the field. If the proton completes 10 revolution by the time it cross the region shown, ‘l’ is close to (mass of proton =1.67×1027 kg , charge of the proton =1.6×10−19 C )
View Solution
