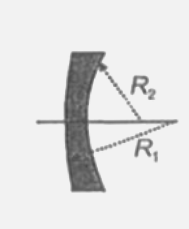
For convex lens, the radii of curvatures of the first and second surface are R1andR2 respectively. Using new Cartesian sign conventions they are
−R1,−R2
−R1,+R2
+R1,+R2
+R1,−R2
The correct Answer is:D
Step by step video, text & image solution for For convex lens, the radii of curvatures of the first and second surface are R_(1) and R_(2) respectively. Using new Cartesian sign conventions they are by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICSBOOK - TARGET PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - CRITICALTHINKING
34 Videos
- RAY OPTICSBOOK - TARGET PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - COMPETITIVE THINKING
60 Videos
- MEASUREMENTSBOOK - TARGET PUBLICATIONCHAPTER - MEASUREMENTSEXERCISE - EVALUATION TEST
17 Videos
- REFRACTION OF LIGHT BOOK - TARGET PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - EVALUATION TEST
12 Videos
Similar Questions
Lens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
Let the given biconvex lens be divided in two equal parts, as shown in Fig. (a), along a section YY' which is perpendicular to the principal axis of lens. What is the power of each part?

View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If two lens parts obtained in (b) are joined together as shown in Fig. (c), (i) what is the net power of the combination?
View Solution
Knowledge Check
A biconvex lens made of material with refractive index n2. The radii of curvatures of its left surface and right surface are R1 and R2. The media on its left and right have refreactive indices n1 and n3 respectively. The first and second focal lengths of the lens are respectively f1 and f2.
Assume that R1=R2,n1≠n3. The ratio, f1/f2, of the two focal lengths is equal toA1Bn1/n3Cn3/n1D(n3−1)/(n1−1)A biconvex lens made of material with refractive index n2. The radii of curvatures of its left surface and right surface are R1 and R2. The media on its left and right have refreactive indices n1 and n3 respectively. The first and second focal lengths of the lens are respectively f1 and f2.
The ratio, f1/f2, of the two focal lengths is equal toAn1/n3B(n1−1)/(n3−1)C(n1+1)/(n3+1)D(n2−n3)/(n2−n1)A biconvex lens made of material with refractive index n2. The radii of curvatures of its left surface and right surface are R1 and R2. The media on its left and right have refreactive indices n1 and n3 respectively. The first and second focal lengths of the lens are respectively f1 and f2.
Assume that n1=n3. Which of the following statements is not correct ?Af1=f2.Bf3 is inversely proportional to n3−1.CIf R1 and R2 are unequal, the focal length would depend on the direction in which light travels through the lens.Df1 may be negative if n1>n2.
All questions refer to the diagram given below. The denoted lines represent the two surfaces of a lens that may be plane or curved. R1 and R2 are the radii of curvature of the surfaces on the left and right respectively. The refractive index of the medium to the left of the lens is n1, that of the material of the lens itself is n2, and that of the medium to the lens is n3. The first and second focal lengths of the lens are f1 and f2 respectively.
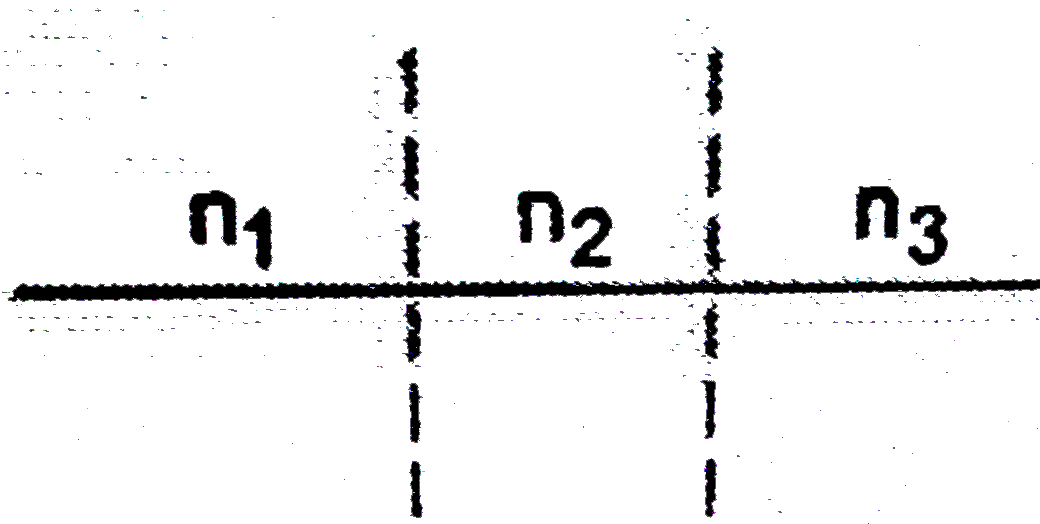
Column A contains certain conditions and column B contains some results which may follow from such conditions.
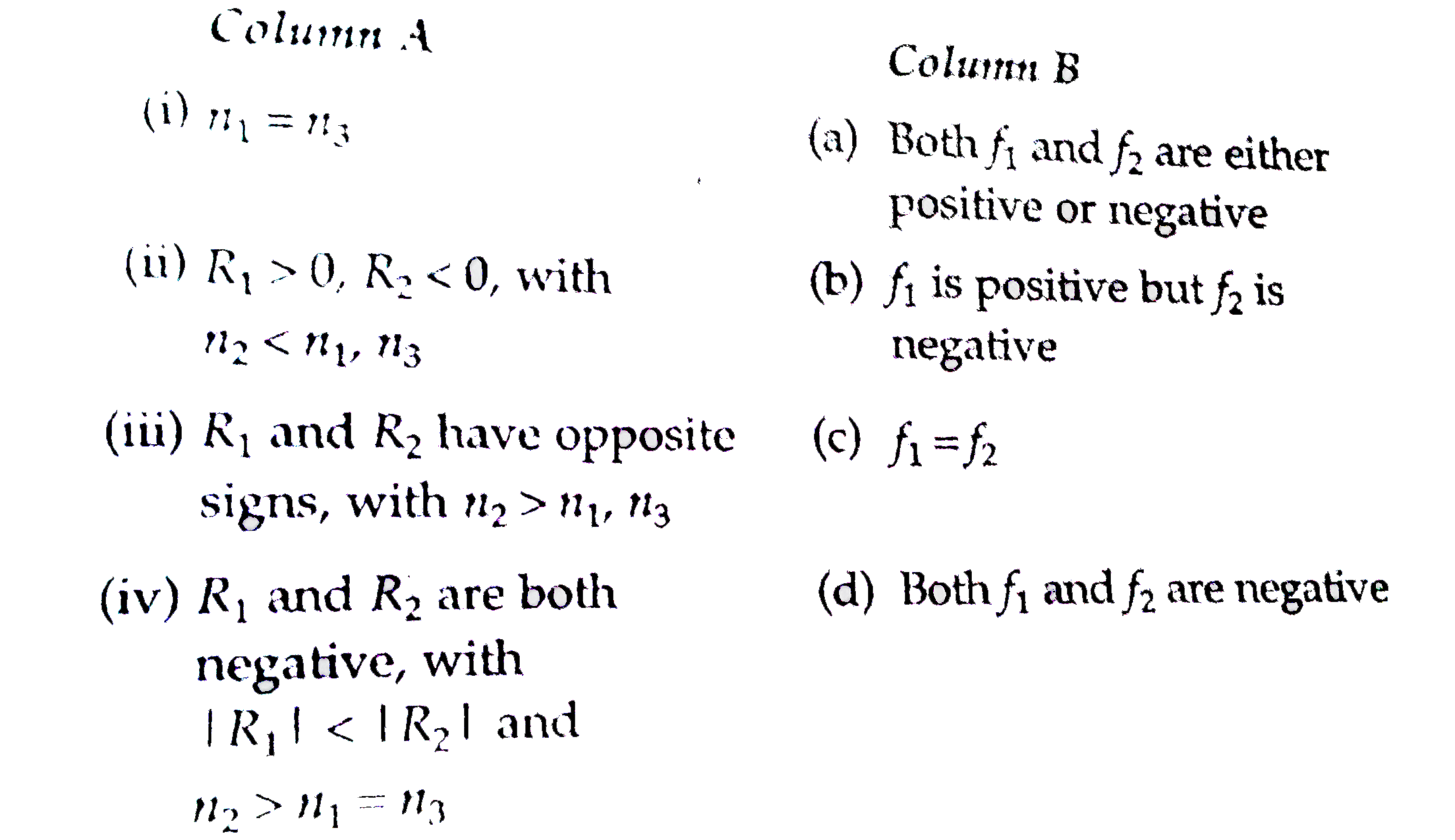
View SolutionIf R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is your answer modified if the given biconvex lens is divided into two parts along a section XX' along its principal axis ?
View SolutionOne surface of a lens is convex and the other is concave, if the radii of curvature are r1 and r2 respectively, the lens will be convex if
View SolutionA convex lens has the same radius of curvature (R ) for both the surfaces. For what value of the refractive index of the material of the convex lens, the numerical values of f and R are equal ?
View Solution
