Two indentical beakers, one filled with water μ=43 and the other filled with oil (μ=1.6) are viewed from directly above. On comparison, which of the following statements is correct?
Water filled beaker appears deeper by a factor of 1.2
Oil filled beaker appear deeper by a factor of 1.2.
Water filled beaker appears deeper by a factor of 43
Oil filled beaker appears deeper by a factor of 1.6.
The correct Answer is:A
To solve the problem, we need to compare the effective heights of the water and oil in the beakers when viewed from directly above. The refractive indices of water and oil are given, and we will use these to determine how deep each liquid appears.
1. Identify the Refractive Indices:
- Refractive index of water, μwater=43
- Refractive index of oil, μoil=1.6
2. Understand the Concept of Apparent Depth:
- The apparent depth of a liquid when viewed from above is given by the formula:
Apparent Depth=hμ
where h is the actual depth of the liquid.
3. Calculate the Apparent Depth of Water:
- Let the actual height of the water be h.
- The apparent depth of water is:
Apparent Depthwater=h43=3h4
4. Calculate the Apparent Depth of Oil:
- The apparent depth of oil is:
Apparent Depthoil=h1.6
5. Compare the Apparent Depths:
- To compare the two apparent depths, we can express them in terms of h:
- For water: 3h4
- For oil: h1.6
- To find out which is deeper, we can set up the ratio:
Apparent DepthwaterApparent Depthoil=3h4h1.6=3h⋅1.64h=3⋅1.64=4.84=1.2
6. Conclusion:
- The apparent depth of water is 1.2 times the apparent depth of oil. Thus, when viewed from above, the water appears deeper than the oil.
Final Answer:
The water beaker will appear 1.2 times deeper than the oil beaker.
- Refractive index of water, μwater=43
- Refractive index of oil, μoil=1.6
- The apparent depth of a liquid when viewed from above is given by the formula:
Apparent Depth=hμ
where h is the actual depth of the liquid.
- Let the actual height of the water be h.
- The apparent depth of water is:
Apparent Depthwater=h43=3h4
- The apparent depth of oil is:
Apparent Depthoil=h1.6
- To compare the two apparent depths, we can express them in terms of h:
- For water: 3h4
- For oil: h1.6
- To find out which is deeper, we can set up the ratio:
Apparent DepthwaterApparent Depthoil=3h4h1.6=3h⋅1.64h=3⋅1.64=4.84=1.2
- The apparent depth of water is 1.2 times the apparent depth of oil. Thus, when viewed from above, the water appears deeper than the oil.
The water beaker will appear 1.2 times deeper than the oil beaker.
Topper's Solved these Questions
- REFRACTION OF LIGHT BOOK - TARGET PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - EVALUATION TEST
12 Videos
- REFRACTION OF LIGHT BOOK - TARGET PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - CRITICAL THINKING
53 Videos
- RAY OPTICSBOOK - TARGET PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - EVALUATION TEST
14 Videos
- SCALARS AND VECTORSBOOK - TARGET PUBLICATIONCHAPTER - SCALARS AND VECTORSEXERCISE - Evaluation Test
19 Videos
Similar Questions
Suhana takes three beakers, A, B and C filled with aqueous solutions of glucose, alcohol and hydrochloric acid repectively as shown in the following figure.
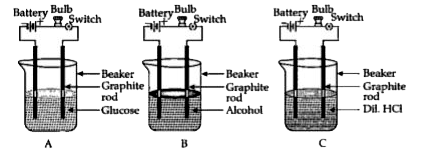
Which of the following statement is correct in terms of glowing of bulb when the switch is ON?
View SolutionTake two identical 100cm3 beakers. Fill one beaker completely with water and the other with kerosence oil. Place the beakers in the scale pans of an ordinary beam balance. It is observed that the beaker filled with water have more mass than the beaker filled with kerosene oil. This is because
View Solution
Knowledge Check
When a fresh eggs is put into a beaker filled with water, it sinks. When the same egg is put in a strong salty water, then if floats. Which of the following is the incorrect statement in this context?
Asalt water enters into egg by osmosis and makes it lighterBsalt water exerts more buoyant forceCsalt water is dense then tap waterDupthrust exerted by a liquid depends on its densityTwo beakers of capacity 500 mL were taken. One of these beakers, labelled as "A", was filled with 400 mL water whereas the beaker labelled "B" was filled with 400 mL of 2 m solution of NaCI. At the same temperature, both the beakers were placed in closed containers of same material and same capacity as shown in Fig. At a given temperature, which of the following staements is correct about the vapor pressure of pure water and that of NaCI solution ?
 AVapour pressure in beaker (A) is more than that in beaker (B).BVapour pressure in beaker (A) is less than that in beaker (B).CVapour pressure is equal in both the beakers.Dvapour presure in beaker (B) is twice the vapour pressure in beaker (A).
AVapour pressure in beaker (A) is more than that in beaker (B).BVapour pressure in beaker (A) is less than that in beaker (B).CVapour pressure is equal in both the beakers.Dvapour presure in beaker (B) is twice the vapour pressure in beaker (A).Two strings , one thick and other thin are connected as shown in Fig.
Which of the following statement(s) is correct with regard to above arrangement?
 AIf a wave is travelling fom string 1 to string 2 , then the joint would be treated as free end.BIf a wave is travelling fom string 1 to string 2 , then the joint would be treated as a fixed end.CIf a wave is travelling fom string 2 to string 1 , then the joint would be treated as free end.DBoth (b) and ( c) are correct.
AIf a wave is travelling fom string 1 to string 2 , then the joint would be treated as free end.BIf a wave is travelling fom string 1 to string 2 , then the joint would be treated as a fixed end.CIf a wave is travelling fom string 2 to string 1 , then the joint would be treated as free end.DBoth (b) and ( c) are correct.
Two identical beakers are filled with water. One of them has an ice block floating in it. The level of water in both the beakers is same. Which beaker will weigh more? Will your answer change if water is replaced with a liquid of higher density in the beakers?
View SolutionThe number of sides of two regular polygons are in the ratio 5:4. The difference between their interior angles is 9∘. Consider the following statements :
1. One of them is a pentagon and the other is a rectangle.
2. One of them is a decagon and the other is an octagon.
3. The sum of their exterior angles is 720∘.
Which of the above statements is/are correct ?
View SolutionA pond of depth 20cm is half filled with an oil of μ=1.4 and the other half is filled with water of refractive index 1.33. Calculate apparent depth of the tank when viewed normally.
View SolutionThe line through the points (4, 3) and (2, 5) cuts off intercepts of length λ and μ on the axes. Which one of the following is correct ?
View SolutionA vessel of depth x is half filled with oil of refractive index μ1 and the other half is filled with water of refractive index μ2. The apparent depth of the vessel when viewed above is
View Solution
