The distance travelled by a ray of light in two media, in the same time are in the ratio 2 : 3. The ratio of refractive index of the first medium to second medium is
3:2
4:9
2:3
9:8
The correct Answer is:A
To solve the problem, we need to find the ratio of the refractive indices of two media based on the distances traveled by light in those media in the same time.
1. Understanding the Given Ratio:
We are given that the distances traveled by a ray of light in two media are in the ratio of 2:3. Let's denote:
- Distance in medium 1 (d1) = 2x
- Distance in medium 2 (d2) = 3x
where x is a common factor.
2. Using the Relation of Speed:
The speed of light in a medium is given by the formula:
v=dt
Since the time (t) taken in both media is the same, we can write:
v1v2=d1d2
Substituting the distances:
v1v2=2x3x=23
3. Relating Refractive Index to Speed:
The refractive index (μ) of a medium is defined as:
μ=cv
where c is the speed of light in vacuum (or air) and v is the speed of light in the medium. For two media, we can write:
μ1μ2=v2v1
4. Substituting the Speed Ratio:
From our earlier step, we found that:
v1v2=23
Therefore, the inverse gives:
v2v1=32
5. Finding the Ratio of Refractive Indices:
Now substituting this into the refractive index ratio:
μ1μ2=v2v1=32
Final Answer:
The ratio of the refractive index of the first medium to the second medium is:
μ1μ2=32
We are given that the distances traveled by a ray of light in two media are in the ratio of 2:3. Let's denote:
- Distance in medium 1 (d1) = 2x
- Distance in medium 2 (d2) = 3x
where x is a common factor.
The speed of light in a medium is given by the formula:
v=dt
Since the time (t) taken in both media is the same, we can write:
v1v2=d1d2
Substituting the distances:
v1v2=2x3x=23
The refractive index (μ) of a medium is defined as:
μ=cv
where c is the speed of light in vacuum (or air) and v is the speed of light in the medium. For two media, we can write:
μ1μ2=v2v1
From our earlier step, we found that:
v1v2=23
Therefore, the inverse gives:
v2v1=32
Now substituting this into the refractive index ratio:
μ1μ2=v2v1=32
The ratio of the refractive index of the first medium to the second medium is:
μ1μ2=32
Topper's Solved these Questions
- REFRACTION OF LIGHT Book:TARGET PUBLICATIONChapter:REFRACTION OF LIGHT Exercise:COMPETITIVE THINKING
Explore 80 Videos
- REFRACTION OF LIGHT Book:TARGET PUBLICATIONChapter:REFRACTION OF LIGHT Exercise:EVALUATION TEST
Explore 12 Videos
- REFRACTION OF LIGHT Book:TARGET PUBLICATIONChapter:REFRACTION OF LIGHT Exercise:EVALUATION TEST
Explore 12 Videos
- RAY OPTICSBook:TARGET PUBLICATIONChapter:RAY OPTICSExercise:EVALUATION TEST
Explore 14 Videos
- SCALARS AND VECTORSBook:TARGET PUBLICATIONChapter:SCALARS AND VECTORSExercise:Evaluation Test
Explore 19 Videos
Similar Questions
Define the refraction index of the second medium with respect to the first medium.
View SolutionA ray of light is incident obliquely at a boundary separating two media . What is its behaviour if (1) the refractive index of the second medium is grater than that of the first medium (2) the refractive index of the first medium is greater that that of the second medium ? Draw the corresponding neat and labelled diagrams.
View Solution
Knowledge Check
A ray of light is travelling from medium A to medium B . The refractive index of the medium B does not depend upon
Anature of the mediumBwavelength of the light usedCnature of the medium ADangle of incidenceA ray of light travelling in air is incident at 45∘ on a medium of refractive index √2. The angle of refractive in the medium is
AA. 45∘BB.60∘CC.30∘DD.70∘Figure shows a ray of light as it travels from medium A to medium B. Refractive index of the medium B relative to medium A is
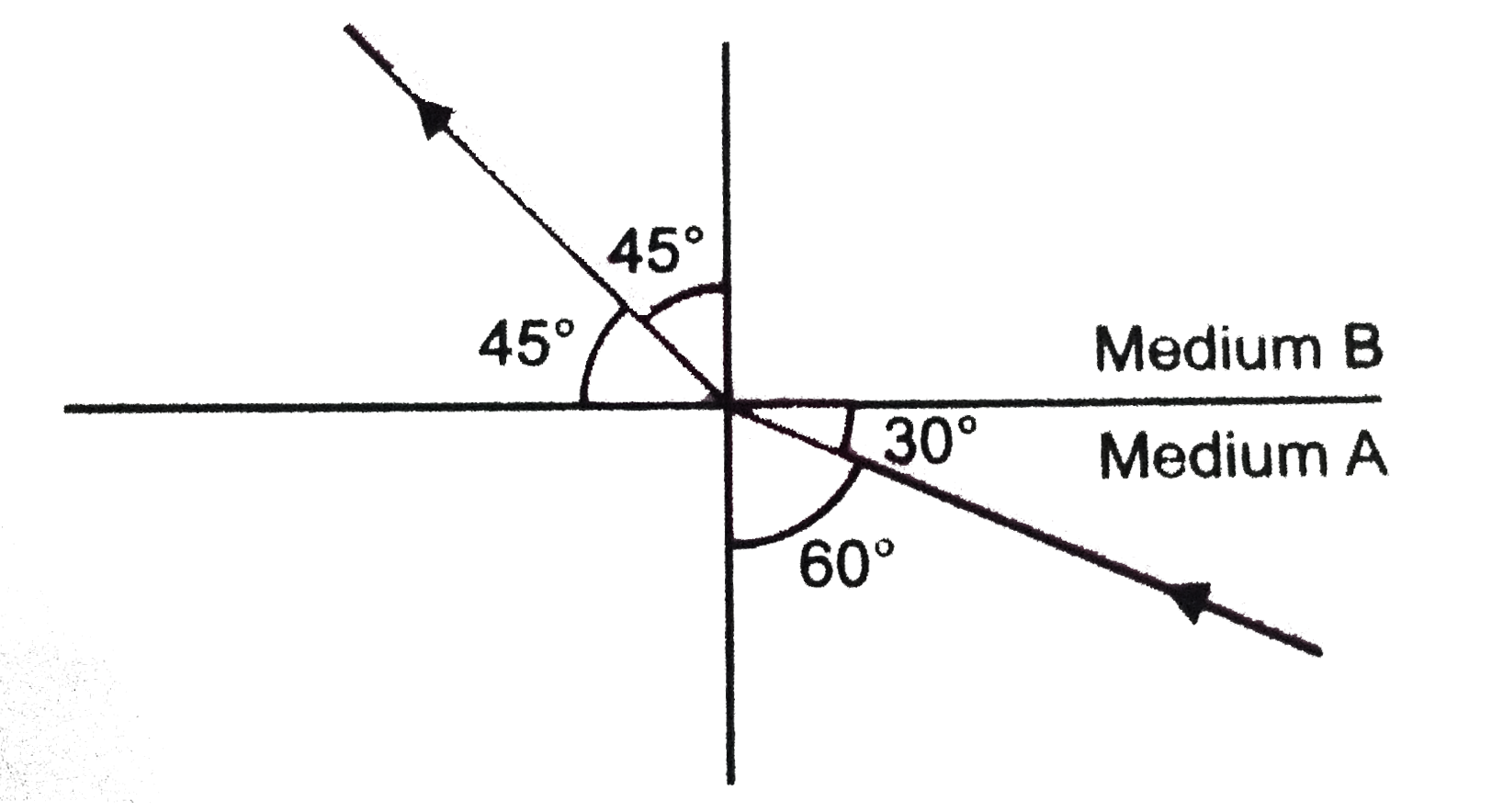 A√3/√2B√2/√3C1/√2D√2
A√3/√2B√2/√3C1/√2D√2
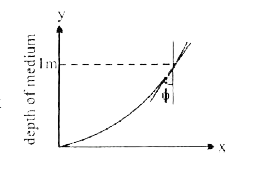
A ray of light travelling in air is incident at grazing angle (incidence angle =90∘) on a medium whose refractive index depends on the depth of the medium. The trajectory of the light in the medium is a parabola, y=2x2. Find, at a depth of 1 m in the medium
(i) the refractive index of the medium and
(ii) angle of incidence ϕ.
View SolutionWhat happens to a ray of light when it travels from one medium to another having equal refractive index ?
View SolutionFigure shows a ray of light as it travels from medium A to medium B. Refractive index of the medium B relative to medium A is

View SolutionFigure shows a ray of light as it travels from medium A to medium B. Refractive index of the medium B relative to medium A is

View SolutionA ray of light is incident obliquely on medium 1 and then passes through two media namely 2 and 3 before emerging into medium 1 again.

The refractive index of medium 3 respect to medium 1 is:
View Solution

