A fish in water (refractive index n ) looks at a bird vertically above in the air. If y is the height of the bird and x is the depth of the fish from the surface, then the distance of the bird as estimated by the fish is
x+y(1+1n)
y+x(1−1n)
y+x(1−1n)
x+y(1−1n)
The correct Answer is:D
To solve the problem, we need to determine the distance of the bird as estimated by the fish, taking into account the refraction of light at the water-air interface. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a fish located at a depth x below the water surface and a bird at a height y above the water surface. The refractive index of water is n.
Step 2: Identify the Refraction Effect
When light travels from a denser medium (water) to a rarer medium (air), it bends away from the normal. The apparent position of the bird as seen by the fish will be shifted due to this refraction.
Step 3: Calculate the Normal Shift
The normal shift can be calculated using the formula:
Normal Shift=y⋅(n−1)
This shift accounts for how much the light bends as it exits the water.
Step 4: Determine the Apparent Height of the Bird
The apparent height of the bird as perceived by the fish will be the actual height y plus the normal shift:
Apparent Height=y+y⋅(n−1)=y+(n−1)y=ny
Step 5: Calculate the Total Distance Perceived by the Fish
The total distance from the fish to the bird, as estimated by the fish, will be the sum of the depth of the fish x and the apparent height of the bird:
Distance=x+ny
Final Result
Thus, the distance of the bird as estimated by the fish is:
Distance=x+ny
We have a fish located at a depth x below the water surface and a bird at a height y above the water surface. The refractive index of water is n.
When light travels from a denser medium (water) to a rarer medium (air), it bends away from the normal. The apparent position of the bird as seen by the fish will be shifted due to this refraction.
The normal shift can be calculated using the formula:
Normal Shift=y⋅(n−1)
This shift accounts for how much the light bends as it exits the water.
The apparent height of the bird as perceived by the fish will be the actual height y plus the normal shift:
Apparent Height=y+y⋅(n−1)=y+(n−1)y=ny
The total distance from the fish to the bird, as estimated by the fish, will be the sum of the depth of the fish x and the apparent height of the bird:
Distance=x+ny
Thus, the distance of the bird as estimated by the fish is:
Distance=x+ny
Topper's Solved these Questions
- REFRACTION OF LIGHT BOOK - TARGET PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - COMPETITIVE THINKING
80 Videos
- REFRACTION OF LIGHT BOOK - TARGET PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - EVALUATION TEST
12 Videos
- REFRACTION OF LIGHT BOOK - TARGET PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - EVALUATION TEST
12 Videos
- RAY OPTICSBOOK - TARGET PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - EVALUATION TEST
14 Videos
- SCALARS AND VECTORSBOOK - TARGET PUBLICATIONCHAPTER - SCALARS AND VECTORSEXERCISE - Evaluation Test
19 Videos
Similar Questions
A fish is 60 cm under water (μ=4/3). A bird directly overhead looks at the fish. If the bird is at a distance of 120 cm from the water surface, (a) What is the apparent position of the fish as seen by the bird and (b) what is the apparent position of the bird as seen by the fish?
View SolutionFind out the following in the figure shown below :

(a) The apparent distance of the fish from the surface as observed by the bird
(b) The apparent distance of the bird from the surface as observed by the fish
View Solution
Knowledge Check
A turtle in water (refractive index μ) looks at a stationary cloud vertically above in the air. If h is the height of the cloud and d is the depth of the fortle from the surface, then the distance of the clond as estimated by the turfle is
Ad+h(1+1μ)Bh+d(1−1μ)Cd+h(1−1μ)Dd+μhA bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
Ah1+h2Bh1+h2μCμh1+h2Dμh1+μh2A fish in a lake (refractive index 4/3 for water ) is viewed through a convex lens. From water surface, the lens is placed in air at half of the distance of the fish from the water surface, so that the image is formed at the fish itself. The focal length of the lens is how many times the depth of fish in water?
A4B6C7.5D9
A diver under water sees a bird in air, vertically above him. If the actual, height of the bird above the water surface is 'h' , then does it appear at the same height 'h' to the diver ? Explain giving reasons. If μw is the refractive index of water, find the shift in the bird's position as observed by the diver.
View SolutionFind out the following in the figure shown below :
(a) The apparent speed of the fish as observed by the bird
(b) The apparent speed of the bird as observed by the fish
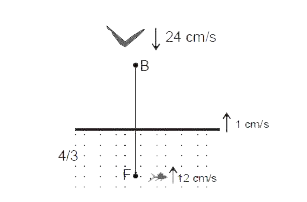
View SolutionA bird in air looks at a fish directly below it inside in a transparent liquid in a tank. If the distance of the fish as estimated by the bird is h1 and that of the bird as estimated by the fish is h2, then the refractive index of the liquid is
View SolutionA bird in air looks at a fish directly below it inside in a transparent liquid in a tank. If the distance of the fish as estimated by the bird is h1 and that of the bird as estimated by the fish is h2, then the refractive index of the liquid is
View SolutionA bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be
View Solution
