Doubtnut Promotions Sticky

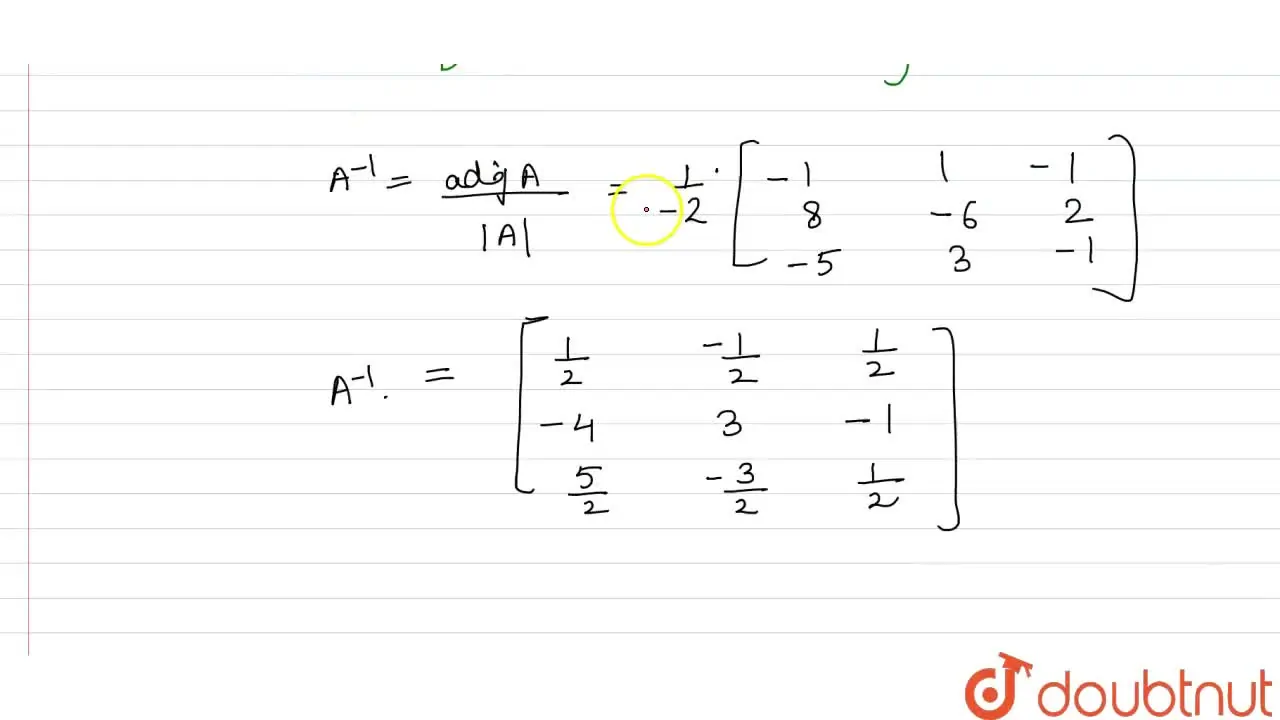
The inverse matrix of A=⎡⎢⎣012123311⎤⎥⎦ is

A

⎡⎢ ⎢ ⎢⎣12−1212−43−152−3212⎤⎥ ⎥ ⎥⎦

B

⎡⎢ ⎢⎣12−4521−6312−1⎤⎥ ⎥⎦

C

12⎡⎢⎣123321423⎤⎥⎦

D

12⎡⎢⎣1−1−1−86−25−31⎤⎥⎦

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:a

|
Answer

Step by step video, text & image solution for The inverse matrix of A=[(0,1,2),(1,2,3),(3,1,1)] is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSMATRICES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The inverse of A=⎡⎢⎣012123311⎤⎥⎦ is

    A12[−1,1,−1),(8,−6,2),(−5,3,−1)]
    B12⎡⎢⎣1−11−86−25−31⎤⎥⎦
    C12⎡⎢⎣111111111⎤⎥⎦
    DNone of these
  • Question 2 - Select One

    The inverse of the matrix ⎡⎢⎣111102311⎤⎥⎦ is

    A14⎡⎢⎣−2025−121−1−2⎤⎥⎦
    B14⎡⎢⎣−2025−2−112−1⎤⎥⎦
    C14⎡⎢⎣−20225−1−2−11⎤⎥⎦
    D14⎡⎢⎣−2025−111−2−1⎤⎥⎦
  • Question 3 - Select One

    The elements in the first row and third column of the inverse of the matrix ⎡⎢⎣123012001⎤⎥⎦ is

    A−2
    B0
    C7
    D1