If ABCD is a cyclic quadrilateral, then is equal to
0
The correct Answer is:C
To solve the problem, we need to find the value of cosA+cosB for a cyclic quadrilateral ABCD.
1. Understanding Cyclic Quadrilateral Properties:
In a cyclic quadrilateral, the opposite angles are supplementary. Thus, we have:
A+C=180∘andB+D=180∘
2. Expressing Angles:
From the supplementary angle property, we can express angle C and angle D in terms of angles A and B:
C=180∘−AandD=180∘−B
3. Using Cosine Angle Identity:
We can use the cosine identity for angles:
cos(180∘−θ)=−cos(θ)
Applying this to angles C and D:
cosC=cos(180∘−A)=−cosA
cosD=cos(180∘−B)=−cosB
4. Substituting Back into the Expression:
Now substituting these values into the expression cosA+cosB:
cosA+cosB=−cosC−cosD
5. Final Expression:
Therefore, we can conclude that:
cosA+cosB=−(cosC+cosD)
6. Conclusion:
Since cosC+cosD can be expressed in terms of cosA+cosB, we can say:
cosA+cosB=−(cosC+cosD)
This shows the relationship between the cosines of the angles in a cyclic quadrilateral.
Final Answer:
Thus, the value of cosA+cosB is equal to:
−cosC−cosD
In a cyclic quadrilateral, the opposite angles are supplementary. Thus, we have:
A+C=180∘andB+D=180∘
From the supplementary angle property, we can express angle C and angle D in terms of angles A and B:
C=180∘−AandD=180∘−B
We can use the cosine identity for angles:
cos(180∘−θ)=−cos(θ)
Applying this to angles C and D:
cosC=cos(180∘−A)=−cosA
cosD=cos(180∘−B)=−cosB
Now substituting these values into the expression cosA+cosB:
cosA+cosB=−cosC−cosD
Therefore, we can conclude that:
cosA+cosB=−(cosC+cosD)
Since cosC+cosD can be expressed in terms of cosA+cosB, we can say:
cosA+cosB=−(cosC+cosD)
This shows the relationship between the cosines of the angles in a cyclic quadrilateral.
Thus, the value of cosA+cosB is equal to:
−cosC−cosD
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLES Book:TARGET PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLES Exercise:CRITICAL THINKING
Explore 60 Videos
- TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLES Book:TARGET PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLES Exercise:COMPETITIVE THINKING
Explore 101 Videos
- STRAIGHT LINE Book:TARGET PUBLICATIONChapter:STRAIGHT LINE Exercise:EVALUATION TEST
Explore 10 Videos
- TRIGONOMETRIC FUNCTIONS Book:TARGET PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONS Exercise:EVALUATION TEST
Explore 10 Videos
Similar Questions
Knowledge Check
If ABCD is a cyclic quadrilateral then what is sinA+sinB−sinC−sinD equal to ?
A0B1C2D2(sinA+sinB)If ABCD is a cyclic quadrilateral, then the value of cosA-cosB+cosC-cosD is equal to
A0B1C2(cosB-cosD)D2(cosA-cosC)In the adjoining figure, if ABCD is a cyclic quadrilateral, find the value of x.
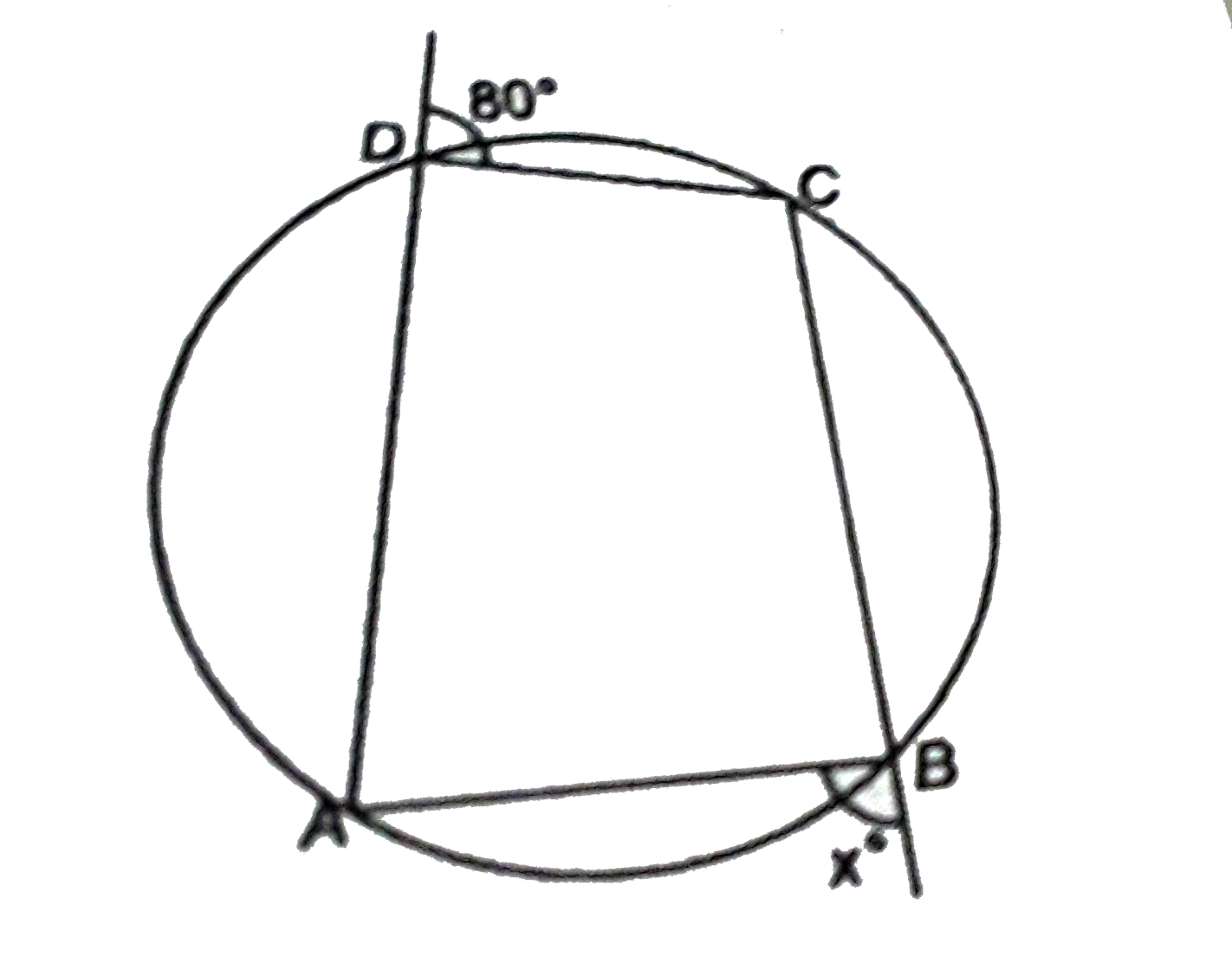 A60∘B80∘C100∘D120∘
A60∘B80∘C100∘D120∘
If ABCD is a quadrilateral then tan(A+B4)
View Solutionif ABCD is a cyclic quadrilateral, then find the value of cosA cosB - cos C cos D.
View SolutionIf ABCD is a cyclic quadrilateral, then tanA+tanC=_________.
View SolutionIf ABCD is a cyclic quadrilateral, then find the value of sinA+sinB−sinC−sinD
View SolutionIn Figure, ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If (∠ADC)=1300, find ∠BAC
View Solution