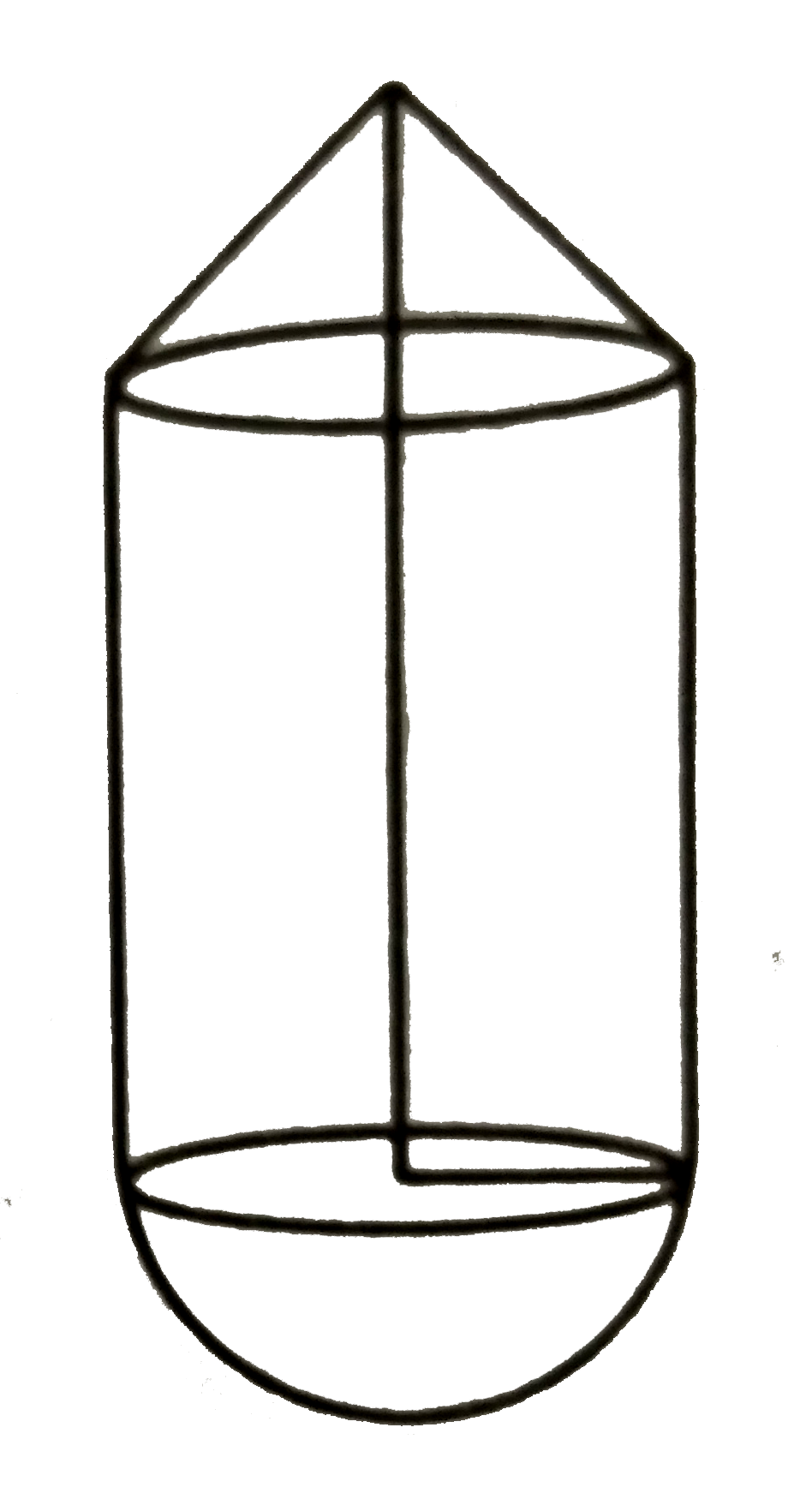
A toy is a combination of a cylinder, hemisphere and a cone, each with radius 10 cm as shown in the figure. Height of the conical part is 10 cm and total height is 60 cm. Find the total surface area of the toy. (π=3.14,√2=1.41)
The correct Answer is:3386.74cm2
Step by step video & image solution for A toy is a combination of a cylinder, hemisphere and a cone, each with radius 10 cm as shown in the figure. Height of the conical part is 10 cm and total height is 60 cm. Find the total surface area of the toy. (pi = 3.14, sqrt(2)= 1.41) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBook:TARGET PUBLICATIONChapter:MENSURATIONExercise:Additional Problems for Practice (Based on Practice Set 7.2)
Explore 6 Videos
- MENSURATIONBook:TARGET PUBLICATIONChapter:MENSURATIONExercise:Additional Problems for Practice (Based on Practice Set 7.3)
Explore 9 Videos
- MENSURATIONBook:TARGET PUBLICATIONChapter:MENSURATIONExercise:Multiple Choice Questions
Explore 31 Videos
- LINEAR EQUATIONS IN TWO VARIABLES Book:TARGET PUBLICATIONChapter:LINEAR EQUATIONS IN TWO VARIABLES Exercise:Chapter Assessment
Explore 20 Videos
- MODEL QUESTION PAPERBook:TARGET PUBLICATIONChapter:MODEL QUESTION PAPERExercise:Questions
Explore 23 Videos
Similar Questions
The base radius of a cylinder is 14 cm and its heights is 30 cm. Find :
(a) volume (b) curved surface area (c) total surface area
View SolutionA toy is in the form of a cone mounted on the hemisphere with the same radius. The diameter of the base of the conical portion is 12 cm and its height is 8 cm.
What is the total surface area of the toy?
View Solution
Knowledge Check
A toy is in the form of a cone mounted on a hemisphere. The radius of the hemisphere and that of the cone is 3 cm and height of the cone is 4 cm. The total surface area of the toy is
A75.43 Sq cmB103.71 Sq cmC85.35 Sq cmD120.71 Sq cm
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base of radius 3.5 cm. Find the total surface area of the article.

View SolutionA cylindrical vessel, open at the top, has a radius 10 cm and height 14 cm. Find the total surface area of the vessel. (Take pi = 3.14)
View SolutionFind the total surface area of a hemisphere of radius 10 cm. (Use π=3.14)
View SolutionA toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the base of the conical portion is 6 cm and its height is 4 cm. Determine the surface area of the toy (Use π=3.14 )
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in fig. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm. Find the total surface area of the article.

View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is 100 cm, and its base is of radius 7 cm, find the total surface area of the article.

View SolutionA toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
View Solution

