let P1=⎡⎢⎣100010001⎤⎥⎦,P2=⎡⎢⎣100001010⎤⎥⎦,P3=⎡⎢⎣010100001⎤⎥⎦,P4=⎡⎢⎣010001100⎤⎥⎦,P5=⎡⎢⎣001100010⎤⎥⎦,P6=⎡⎢⎣001010100⎤⎥⎦ and X=6∑k=1Pk⎡⎢⎣213102321⎤⎥⎦PTk Where PTk is transpose of matrix Pk. Then which of the following options is/are correct?
X is a symmetric matrix
if X=⎡⎢⎣111⎤⎥⎦=α⎡⎢⎣111⎤⎥⎦, then α=30
X-30I is an invertible matrix
The sum of diagonal entries of X is 18.
The correct Answer is:A, B, D
To solve the problem step by step, we will analyze the given matrices Pk and the expression for X.
Step 1: Understand the given matrices
The matrices P1,P2,P3,P4,P5,P6 are defined as follows:
P1=⎛⎜⎝100010001⎞⎟⎠,P2=⎛⎜⎝100001010⎞⎟⎠,P3=⎛⎜⎝010100001⎞⎟⎠
P4=⎛⎜⎝010001100⎞⎟⎠,P5=⎛⎜⎝001100010⎞⎟⎠,P6=⎛⎜⎝001010100⎞⎟⎠
Step 2: Define the matrix A
The matrix A is given by:
A=⎛⎜⎝213102321⎞⎟⎠
Step 3: Calculate X
The expression for X is:
X=6∑k=1PkAPTk
Here, PTk is the transpose of the matrix Pk.
Step 4: Verify the symmetry of X
To show that X is symmetric, we need to demonstrate that XT=X.
Using the property of transpose:
XT=(6∑k=1PkAPTk)T=6∑k=1(PkAPTk)T=6∑k=1PTkATPk
Since PTk=Pk (as shown in the video), we have:
XT=6∑k=1PkAPk=X
Thus, X is symmetric.
Step 5: Calculate X⋅⎛⎜⎝111⎞⎟⎠
Let B=⎛⎜⎝111⎞⎟⎠.
We need to compute XB:
XB=6∑k=1PkAPTkB
Since PTkB=PkB and PkB results in a vector that sums the entries of B:
PkB=⎛⎜⎝111⎞⎟⎠ (for all k)
Thus,
XB=6∑k=1PkA⎛⎜⎝111⎞⎟⎠
Calculating A⎛⎜⎝111⎞⎟⎠:
A⎛⎜⎝111⎞⎟⎠=⎛⎜⎝2+1+31+0+23+2+1⎞⎟⎠=⎛⎜⎝636⎞⎟⎠
Thus,
XB=6∑k=1Pk⎛⎜⎝636⎞⎟⎠
This results in:
XB=6⋅⎛⎜⎝111⎞⎟⎠+3⋅⎛⎜⎝111⎞⎟⎠+6⋅⎛⎜⎝111⎞⎟⎠=30⎛⎜⎝111⎞⎟⎠
Thus, α=30.
Step 6: Check if X−30I is invertible
Since XB=30B, we have:
(X−30I)B=0
This implies that X−30I is not invertible.
Step 7: Calculate the trace of X
The trace of X is given by:
trace(X)=trace(P1APT1)+trace(P2APT2)+…+trace(P6APT6)
Each PkAPTk contributes to the trace, and since the trace of a product is invariant under cyclic permutations:
trace(PkAPTk)=trace(A)
Calculating the trace of A:
trace(A)=2+0+1=3
Thus,
trace(X)=6⋅3=18
Conclusion
The correct options are:
1. X is a symmetric matrix.
2. α=30.
3. The sum of diagonal entries of X is 18.
P4=⎛⎜⎝010001100⎞⎟⎠,P5=⎛⎜⎝001100010⎞⎟⎠,P6=⎛⎜⎝001010100⎞⎟⎠
1. X is a symmetric matrix.
2. α=30.
3. The sum of diagonal entries of X is 18.
Topper's Solved these Questions
Similar Questions
Knowledge Check
let P1=⎡⎢⎣100010001⎤⎥⎦,P2=⎡⎢⎣100001010⎤⎥⎦,P3=⎡⎢⎣010100001⎤⎥⎦,P4=⎡⎢⎣010001100⎤⎥⎦,P5=⎡⎢⎣001100010⎤⎥⎦,P6=⎡⎢⎣001010100⎤⎥⎦ and X=6∑k=1Pk⎡⎢⎣213102321⎤⎥⎦PTk Where PTk is transpose of matrix Pk. Then which of the following options is/are correct?
AThe sum of diagonal entries of X is 18BX is a symmetric matrixCX=30I is an invertible matrixDIf X⎡⎢⎣111⎤⎥⎦=α⎡⎢⎣111⎤⎥⎦, then α=30Let P1=I=⎡⎢⎣100010001⎤⎥⎦,P2=⎡⎢⎣100001010⎤⎥⎦
P3=⎡⎢⎣010100001⎤⎥⎦,P4=⎡⎢⎣010001100⎤⎥⎦
P5=⎡⎢⎣001100010⎤⎥⎦,P6=⎡⎢⎣001010100⎤⎥⎦ and
X=6∑k=1PK⎡⎢⎣213102321⎤⎥⎦PTK
Where , PTK denotes the transpose of the matrix PX. then which of the following option is/are correct ?AX is a symmertic matrixBThe sum of diagonal entries of X is 18CX−30I is an invertible matrixDIfX⎡⎢⎣111⎤⎥⎦=α⎡⎢⎣111⎤⎥⎦,then α=30If A=⎡⎢⎣010100001⎤⎥⎦, then A−1=
AAB−AC⎡⎢⎣100010001⎤⎥⎦D⎡⎢⎣100100010⎤⎥⎦
If A=⎡⎢⎣001010100⎤⎥⎦ then A6=
View SolutionThe truth table for the following combination of gates is
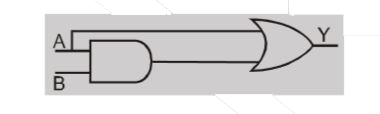
(a) ABY000010101111
(b) ABY000010100111
(c) ABY001011101110
(d) ABY0000111011110
View SolutionIf A=⎡⎢⎣0010−10100⎤⎥⎦ then A−1=
View SolutionIf P=⎡⎢⎣124310001⎤⎥⎦,Q=⎡⎢⎣1−2−3−31900−5⎤⎥⎦then (PQ)−1 equals to
View SolutionA=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦
A−1=16(A2+CA+DI) then C and D equal to
View Solution

