If ˆa is a unit vector and projection of x along ˆa is 2 units and (ˆa×x)+b=x, then x is equal to
12(ˆa−b+(ˆa×b))
12(2ˆa+b+(ˆa×b))
(ˆa+(ˆa×b))
None of these
The correct Answer is:B
Step by step video, text & image solution for If hat(a) is a unit vector and projection of x along hat(a) is 2 units and (hat(a)times x)+b=x, then x is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (More Than One Correct Option Type Questions)
Explore 36 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Statement I And Ii Type Questions)
Explore 12 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise For Session 4
Explore 10 Videos
- PROBABILITYBook:ARIHANT MATHSChapter:PROBABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 55 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
Similar Questions
The scalar product of the vector ˆi+ˆj+ˆkwith a unit vector along the sum of vector 2ˆi+4ˆj−5ˆkand λˆi+2ˆj+3ˆkis equal to one. Find the value of λ.
View SolutionConsiderˆaandˆb be two unit vectors such that ˆa+ˆb is also a unit vector. If the angle between ˆaandˆb is pπ then k is equal to ________
View Solution
Knowledge Check
A unit vector along the direction ˆi+ˆj+ˆk has a magnitude :
A√3B√2C1D0The unit vector along →A=2ˆi+3ˆj is :
A2ˆi+3ˆjB2ˆi+3ˆj2C2ˆi+3ˆj3D2ˆi+3ˆj√13The unit vector along ˆi+ˆj is
AˆkBˆi+ˆjCˆi+ˆj√2Dˆi+ˆj2
The magnitude of the vector product of the vector ˆi+ˆj+ˆk with a unit vector along the sum of vectors 2ˆi+4ˆj− 5ˆk and λi+2ˆj+3ˆk is equal to √2 . Find the value of λ .
View SolutionFind a unit vector perpendicular to the vectors ˆj+2ˆk&ˆi+ˆj
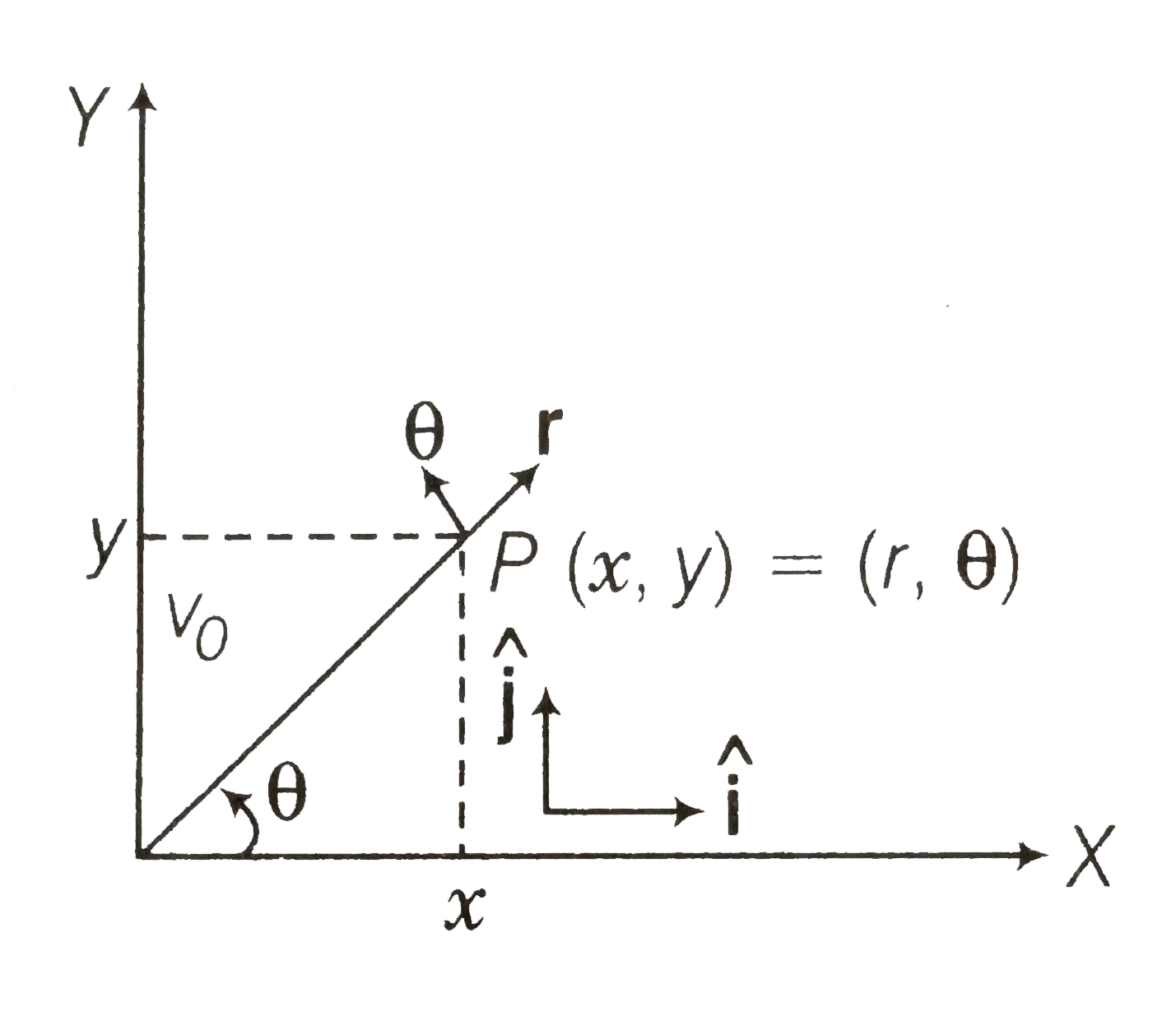
View SolutionMotion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates A=Axˆi+Ayˆj, where ˆi and ˆj are unit vector along x and y-directions, respectively and Ax and Ay are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as A=Arˆr+Aθˆθ, where ˆr=rr=cosθˆi+sinθˆj and ˆθ=−sinθˆi+cosθˆj are unit vectors along direction in which r and θ are increasing.
(a) Express ˆi and ˆj in terms of ˆr and ˆθ.
(b) Show that both ˆr and ˆθ are unit vectors and are perpendicular to each other.
(c) Show that ddt(ˆr)=ωˆθ, where ω=dθdt and ddt(ˆθ)=−θˆr.
(d) For a particle moving along a spiral given by r=aθˆr, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
View SolutionFind the unit vector in the direction of the vector :
→b=2ˆi+ˆj+2ˆk
View SolutionThe scalar product of the vector ˆi+ ˆj+ ˆk with the unit vector along the sum of vectors 2ˆi+ 4ˆj−5ˆk . and λˆi+ 2ˆj+ 3ˆk is equal to one. Find the value of λ .
View Solution

