The moment of the force F acting at a point P, about the point C is
F×CP
CP⋅F
a vector having the same direction as F
CP×F
The correct Answer is:D
To find the moment of the force F acting at point P about point C, we can follow these steps:
Step 1: Understand the Concept of Moment
The moment of a force about a point is defined as the vector product (cross product) of the position vector and the force vector. The formula for the moment M is given by:
M=r×F
where r is the position vector from point C to point P.
Step 2: Define the Position Vector r
The position vector r can be expressed in terms of the position vectors of points P and C:
r=P−C
This means that r is the vector that points from C to P.
Step 3: Substitute r into the Moment Formula
Now, we substitute r into the moment formula:
M=(P−C)×F
Step 4: Calculate the Moment
The moment M can now be calculated using the cross product:
M=P×F−C×F
This expression gives us the moment of the force about point C.
Step 5: Analyze the Direction of the Moment
The direction of the moment vector M is perpendicular to the plane formed by r and F. Therefore, the moment will not be in the same direction as F or C.
Conclusion
Thus, the moment of the force F acting at point P about point C is given by:
M=(P−C)×F
The moment of a force about a point is defined as the vector product (cross product) of the position vector and the force vector. The formula for the moment M is given by:
M=r×F
where r is the position vector from point C to point P.
The position vector r can be expressed in terms of the position vectors of points P and C:
r=P−C
This means that r is the vector that points from C to P.
Now, we substitute r into the moment formula:
M=(P−C)×F
The moment M can now be calculated using the cross product:
M=P×F−C×F
This expression gives us the moment of the force about point C.
The direction of the moment vector M is perpendicular to the plane formed by r and F. Therefore, the moment will not be in the same direction as F or C.
Thus, the moment of the force F acting at point P about point C is given by:
M=(P−C)×F
Topper's Solved these Questions
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (More Than One Correct Option Type Questions)
Explore 36 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Statement I And Ii Type Questions)
Explore 12 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise For Session 4
Explore 10 Videos
- PROBABILITYBook:ARIHANT MATHSChapter:PROBABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 55 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
Similar Questions
Knowledge Check
The moment of the force 5i+10j+16k acting at the point P, 2i−7j+10k about the point O, −5i+6j−10k is
A20i−12j+135kB−408i−12j+135kC20kDnoneA disc is pulled by a force F acting at a point above the centre of mass of the disc.
The direction of frictional force (fr) acting on disc pushed on a rough surface will be represented by.A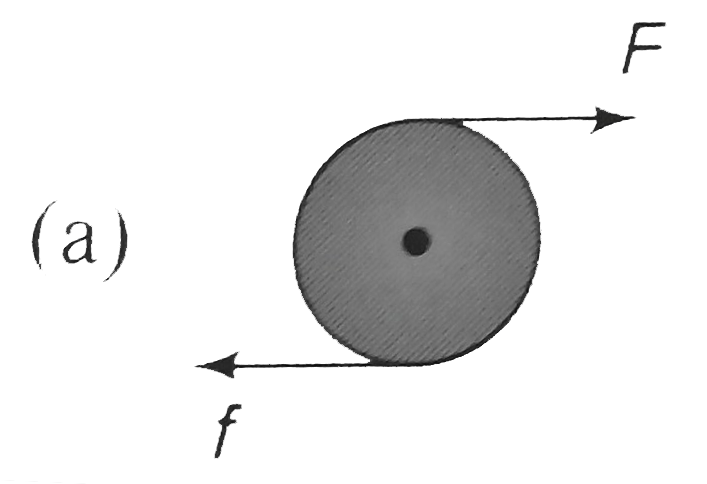 .B
.B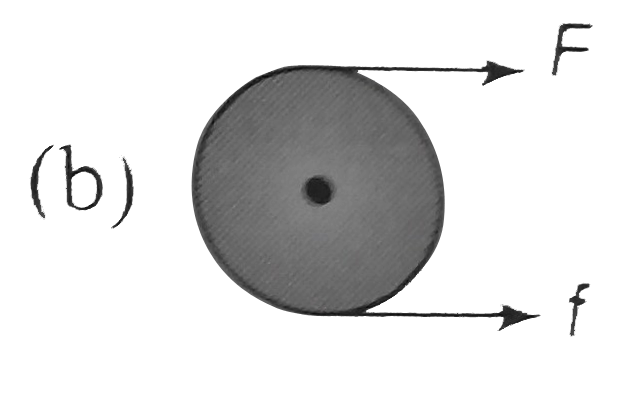 .C
.C .DInformation is insufficient.
.DInformation is insufficient.Force ˆi+2ˆj−3ˆk,2ˆi+3ˆj+4ˆk and −ˆi−ˆj+ˆk are acting at the point P(0,1,2) . The moment of these forces about the point A(1,-2,0) is
A2ˆi−6ˆj+10ˆkB−2ˆi+6ˆj−10ˆkC2ˆi+6ˆj−10ˆkDnone of these
Find the moment of force →F=ˆi+ˆj+ˆk acting at point (−2,3,4) about the point (1,2,3).
View SolutionIf two equal components (P) of a force (F) acting at an angle 120∘, then F is
View SolutionIf two equal components (P) of a force (F) acting at an angle 120∘, then F is
View SolutionMoment of a force of megnitude 20 N acting along positive x direction at point (3m 0, 0) about the point (0, 2, 0) (in N-m) is :-
View SolutionA force √5 units acts along the line x−32=y−4−1 , the moment of the force about the point (4,1) along z-axis is
View Solution