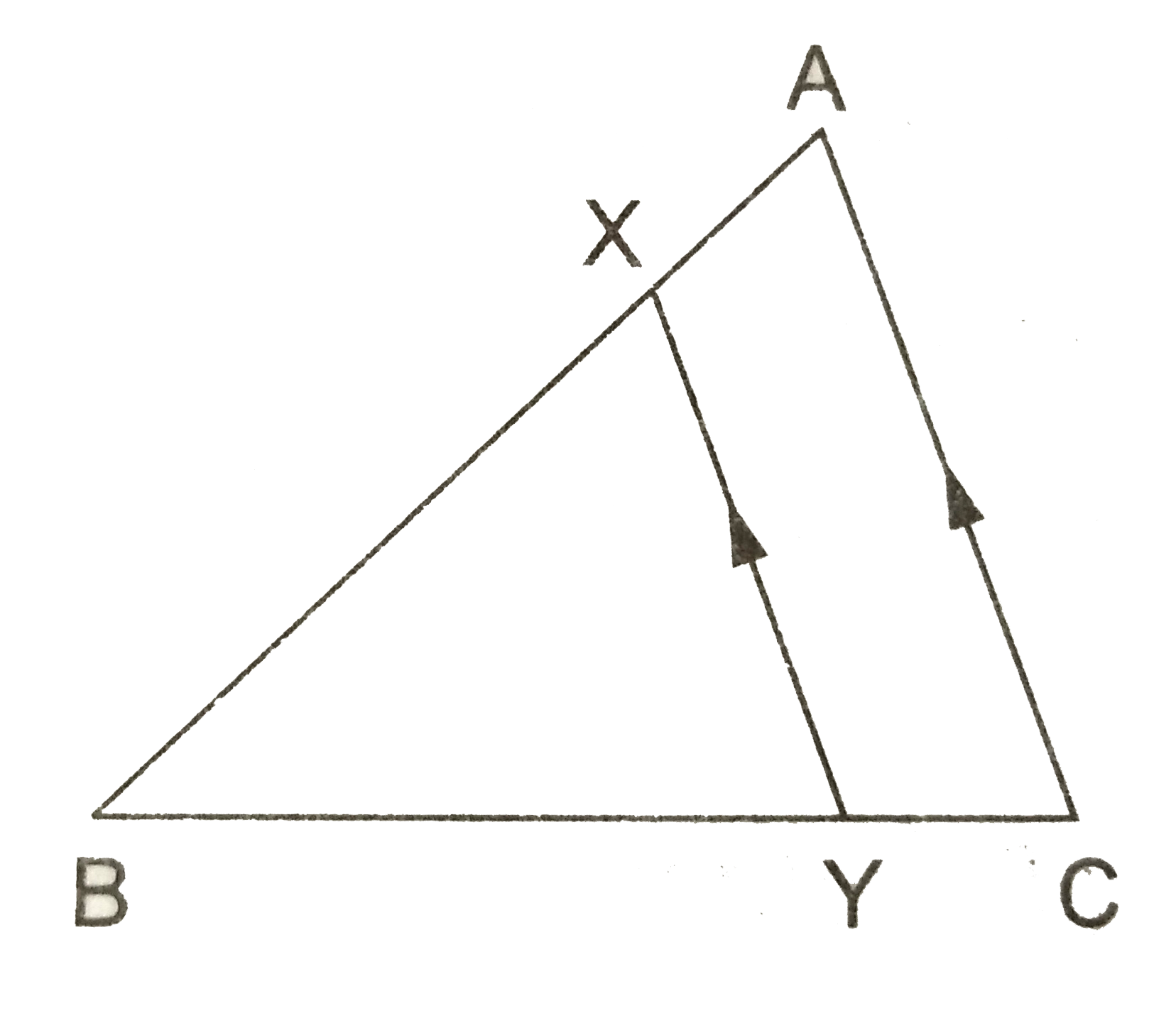In triangle line dividing the triangle ABC into two regions of equal area is perpendicular to AB at point X. Find the value of
The correct Answer is:
Step by step video, text & image solution for In triangle ABC,BC=8,CA=6, and AB=10,A line dividing the triangle ABC into two regions of equal area is perpendicular to AB at point X. Find the value of (BX)/(sqrt2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise For Session 1
Explore 10 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise For Session 2
Explore 10 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBook:ARIHANT MATHSChapter:TRIGONOMETRIC EQUATIONS AND INEQUATIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 12 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 9 Videos
Similar Questions
Knowledge Check
In right △ABC, AB=BC , then ∠A is equal to
A45∘B90∘C60∘DNone of theseIn a triangle ABC, BP is drawn perpendicular to BC to meet CA in P, such that CA = AP, then BPAB=
A2 sin AB2 sin BC2 sin CDnone of theseIn ΔABC, XY is parallel to BC and it divides the triangle into two equal areas (X lies on AB and Y lies on AC) then BX:AB equals
A√2:√2−1B1:1C2:1D√2−1:√2
Consider a triangle ABC with AB=13, BC=14, CA=15. A line perpendicular to BC divides the interior of ΔABC into two regions of equal area. Suppose that the aforesaid perpendicular cuts BC at D, and cuts ΔABC again at E. If L is the length of the line segment DE, find L2.
View SolutionIn a triangle ABC, let AB=√23,BC=4andCA=5 . Then the value of cotA+cotBcotC is
View SolutionIn triangle ABC, BC = 3, CA=5 and AB = 6, then the value of 1+sinAsin A2+cos A2 is equal to
View SolutionIn a triangle ABC, if AB=3, BC=4, CA=5. Then the surface area of the sphere having a radius equal to the inradius of the triangle is.
View SolutionIn a triangle ABC, AB = 8 cm, AC = 10 cm and ∠B=90∘, then the area of ΔABC is
View Solution