If the length of the tangent drawn from (f,g) to the circle x2+y2=6 be twice the length of the tangent drawn from the same point to the circle x2+y2+3(x+y)=0 then show that g2+f2+4g+4f+2=0.
The correct Answer is:f2+g2+4f+4g=−2
Step by step video, text & image solution for If the length of the tangent drawn from (f, g) to the circle x^2+y^2= 6 be twice the length of the tangent drawn from the same point to the circle x^2 + y^2 + 3 (x + y) = 0 then show that g^2 +f^2 + 4g + 4f+ 2 = 0 . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise For Session 1
18 Videos
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise For Session 2
17 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
43 Videos
Similar Questions
If the length of the tangent from (f,g) to the circle x2+y2=6 is twice the length of the tangent from the same point to the circle x2+y2+3x+3y=0, then
View SolutionIf the length of the tangent drawn from (α,β) to the circle x2+y2=6 be twice the length of the tangent from the same point to the circle x2+y2+3x+3y=0, then prove that α2+β2+4α+4β+2=0
View Solution
Knowledge Check
The length of tangent from (5,1) to the circle x2+y2+6x−4y−3=0 is
A7B49C63D21The length of the tangent from (0, 0) to the circle 2(x2+y2)+x−y+5=0, is
A√5B√5/2C√2D√5/2The length of tangent from (5,1) to the circle x2+y2+6x−4y−3=0 is
A7B49C63D21
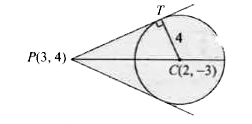
Find the length of a tangent drawn from the point (3,4) to the circle x2+y2−4x+6y−3=0.
View SolutionThe length of the tangent drawn from the point (2,3) to the circle 2(x2+y2)−7x+9y−11=0.
View SolutionThe length of the tangent drawn from the point (2, 3) to the circles 2(x2+y2)–7x+9y–11=0.
View SolutionThe length of tangent from (5,1) to the circle x2+y2+6x−4y−3=0 is
View SolutionThe length of tangent from (5,1) to the circle x2+y2+6x−4y−3=0 is
View Solution