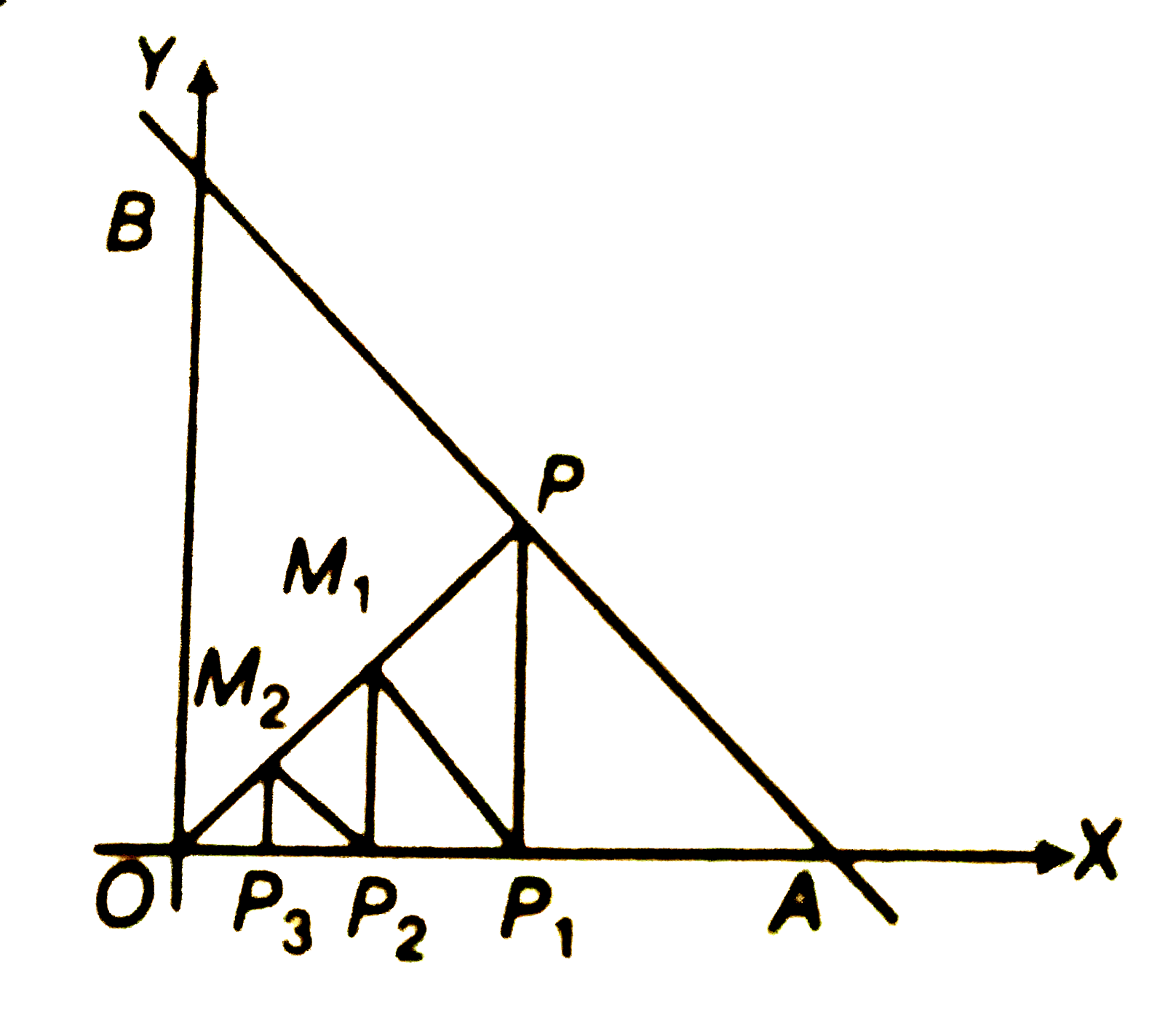
The line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P1 is the foot of perpendicular from P to OA,M1 is that of P1 from OP,P2 is that of M1 from OA,M2 is that of P2 from OP,P3 is that of M2 from OA and so on. If Pn denotes theb nth foot of the perpendicular on OA, then find OPn
The line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P(1) is the foot of perpendicular from P to OA, M(1) is that of P(1) from OP,P(2) is that of M(1) from OA,M(2) is that of P(2) from OP,P(3) is that of M(2) from OA and so on. If P(n) denotes theb nth foot of the perpendicular on OA, then find OP(n) ..

A

12n

B

12n

C

2n−1

D

2n+3

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for The line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P_(1) is the foot of perpendicular from P to OA, M_(1) is that of P_(1) from OP,P_(2) is that of M_(1) from OA,M_(2) is that of P_(2) from OP,P_(3) is that of M_(2) from OA and so on. If P_(n) denotes theb nth foot of the perpendicular on OA, then find OP_(n) . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSTHE STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Consider the plane π1:2x−3y+4z+9=0 and the point P(1,-2,3).
    ocr_image
    A is the foot of perpendicular from P to π1. Equation of PA is _________ .

    Ax−12=y+2−3=z−34
    Bx+12=y−2−3=z+34
    C→r=(ˆi+2ˆj−3ˆk)+λ(2ˆi−3ˆj+4ˆk)
    D→r=(ˆi−2ˆj+3ˆk)+λ(ˆi−2ˆj+3ˆk)

  • The length of the perpendicular from P(1,6,3) to the line x1=y−12=z−23is

    A3
    B√11
    C√13
    D5

  • If the distance of the point P(1,−2,1) from the plane x+2y−2z=α,whereα>0,is5, then the foot of the perpendicular from P to the place is a. (83,43,−73) b. (43,−43,13) c. (13,23,103) d. (23,−13,−53)

    A(83,43,−73)
    B(43,−43,13)
    C(13,23,103)
    D(23,−13,52)