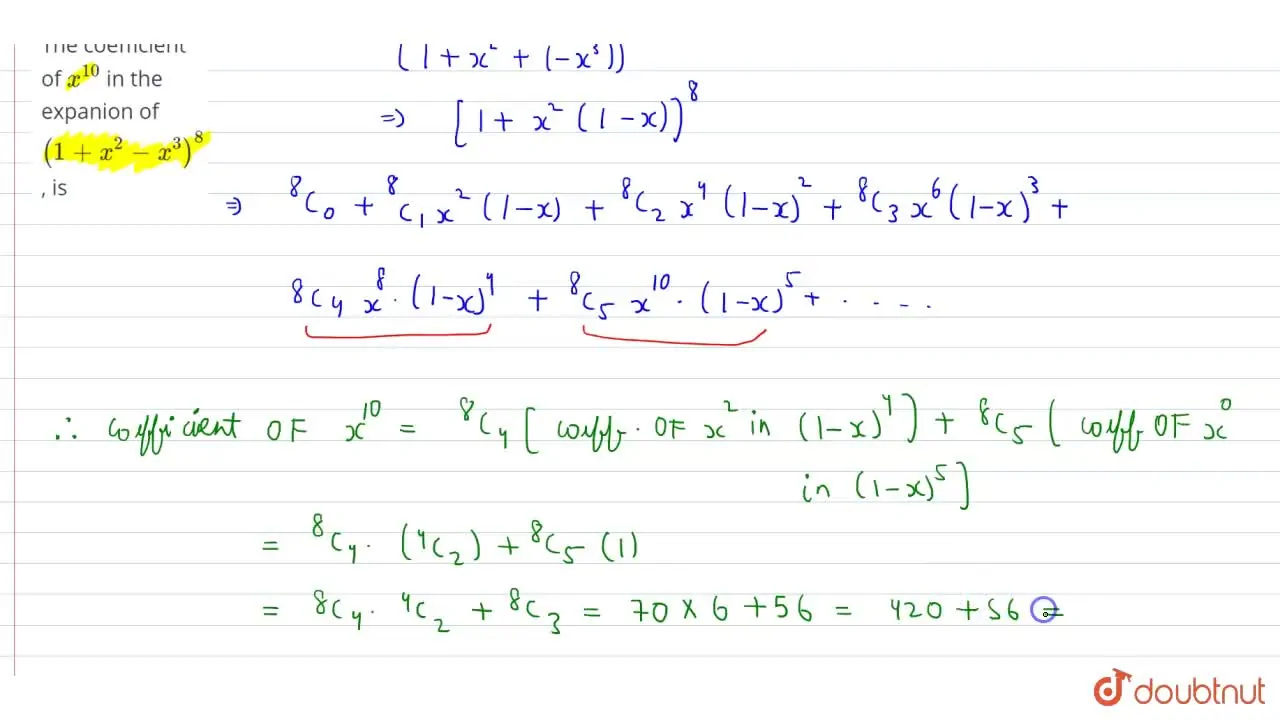The coefficient of x10 in the expanion of
(1+x2−x3)8 , is
A
420
B
476
C
532
D
588
Video Solution
Text Solution
The correct Answer is:b
Given expansion can be rewritten as [1+x2(1−x)]8
=8C0+8C1x2(1−x)+8C2x4(1−x)2
+8C3x6(1−x)3+8C4x8(1−x)4+8C5x10(1−x)5+…
There are only two terms , which we get the coefficient of x10.
∴ Coefficient of x10=8C4 [Coefficient of x2in(1−x)4]
+8C5 [Coefficient of x6in(1−x)5]
=8C4(4C2)+8C5(1)
=(8C4)(4C2)+8C3=(70)(6)+56=476
|
Updated on:21/07/2023
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (More Than One Correct Option Type Questions)15videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Passage Based Questions)21videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 414videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)23videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)16videos
CIRCLE
Similar Questions
The coefficient of x10 in the expanion of
(1+x2−x3)8 , isView SolutionThe coefficient of x10 in the expansion of (1+x2−x3)8 is 476 b. 496 c. 506 d. 528
View SolutionThe coefficient of x10 in the expansion of: (3x2−1x2)15 is:
View SolutionThe coefficient of x10 in the expansion of (1−2x+3x2−4x3+...∞)2 is
View SolutionThe coefficient of x4 in the expansion of (1−x−2x2)8 is
View SolutionThe coefficient of xn in the expansion of (1+x)2(1−x)3, is
View SolutionThe coefficient of x10 in the expanion of
(1+x2−x3)8 , isView SolutionThe coefficient of x7 in the expansion of (1−x−x2+x3)8 is
View SolutionThe coefficient of x8 in the expansion of (1+x+x2+x3)4 is
View SolutionFind the coefficient of x10 in the expansion of (1−x2)10
View Solution