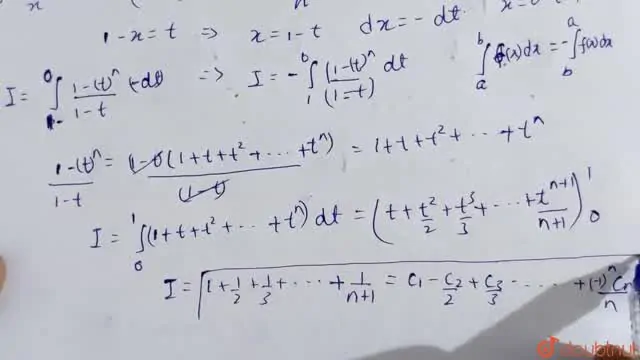If , show that
.
We know that ,
or
Dividing in each side by x , then
On integrating within limits 0 to , we have
Putting 1 - x = t in integral
when
Hence ,
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - JEE Type Solved Example : (Matching Type Questions )2videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 18videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)23videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)16videos
CIRCLE
Similar Questions
If (1+x)n=C0+C1x+C2x2+C3x3+…+Cnxn , prove that
C0−C12+C23−…+(−1)nCnn+1=1n+1.View Solution(1+x)n=C0+C1x+C2x2+C3x3+…+Cnxn , prove
that C0−2C1+3C2−4C3+…+(−1)n(n+1)Cn=0View SolutionIf (1+x)n=C0+C1x+C2x2+C3x3+…+Cnxn prove that
C01+C23+C45+...=2nn+1 .View SolutionIf (1+x)n=C0+C1x+C2x2+C3x3
+...+Cnxn , prove that C12+C34+C56+…=2n+1−1n+1 .View SolutionIf (1+x)n=C0+C1x+C2x2
+C3x3+…+Cnxn , prove that
C21+2C22+3C23+..+nC2n=(2n−1)!((n−1)!)2View SolutionC0−C12+C23−......+(−1)nCnn+1=1n+1
View SolutionIf (1+x)n=C0+C1x+C2x2+…+Cnxn , prove that
C0+2C1+3C2+…+(n+1)Cn=(n+2)2n−1 .View SolutionC0−C12+C23−...............(−1)nCnn+1=1n+1
View SolutionIf (1+x)n=C0+C1x+C2x2+…+C0xn , prove that (1⋅2)C2+(2⋅3)
C3+…+{(n−1)⋅n}Cn=n(n−1)2n−2 .View SolutionIf (1+x)n=C0+C1x+C2x2+...+Cnxn , prove that
C1+2C2+3C3+...+nCn=n⋅2n−1View Solution