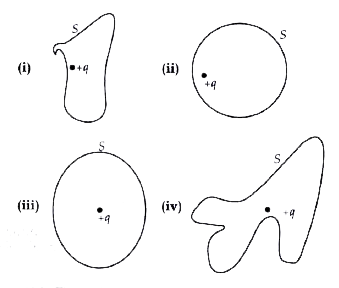If the electric flux entering and leaving an enclosed surface respectively are ϕ1andϕ2, the electric charge inside the surface will be
A
(ϕ2−ϕ1)ε0
B
(ϕ2−ϕ1)ε0
C
(ϕ2−ϕ1)/ε0
D
(ϕ1−ϕ2)/ε0
Video Solution
Text Solution
The correct Answer is:A
From Gauss's law, ϕ2−ϕ1=qε0 ∴q=ε0(ϕ2−ϕ1)
|
Topper's Solved these Questions
- ELECTROSTATICSBook:MARVEL PUBLICATIONChapter:ELECTROSTATICSExercise:TEST YOUR GRASP
Explore 20 Videos
- ELECTRONS AND PHOTONS Book:MARVEL PUBLICATIONChapter:ELECTRONS AND PHOTONS Exercise:TEST YOUR GRASP - 17
Explore 15 Videos
- GRAVITATION Book:MARVEL PUBLICATIONChapter:GRAVITATION Exercise:TEST YOUR GRASP -2
Explore 20 Videos
Similar Questions
Knowledge Check
If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2, the electric charge inside the surface will be
A(a) (ϕ2−ϕ1)εoB(b) (ϕ1+ϕ2)/εoC(c) (ϕ2−ϕ1)/εoD(d) (ϕ1+ϕ2)εoIf the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2, the electric charge inside the surface will be
Aϕ3−ϕ1εnBϕ2+ϕ1εnC(ϕ1−ϕ3)εnDεn(ϕ2−ϕ1)If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2 then the electric charge inside the surface will he
A(ϕ+ϕ2)ε0B(ϕ2−ϕ1)ε0C(ϕ1−ϕ2)ε0D(−ϕ1−ϕ2)ε0
Electric flux through a closed surface in free space enclosing a charge q is
View SolutionIf the electric flux entering and leaving an enclosed surface are ϕ1andϕ2 respectively, then the electric charge present within the surface is
View SolutionThe electric flux through the surface
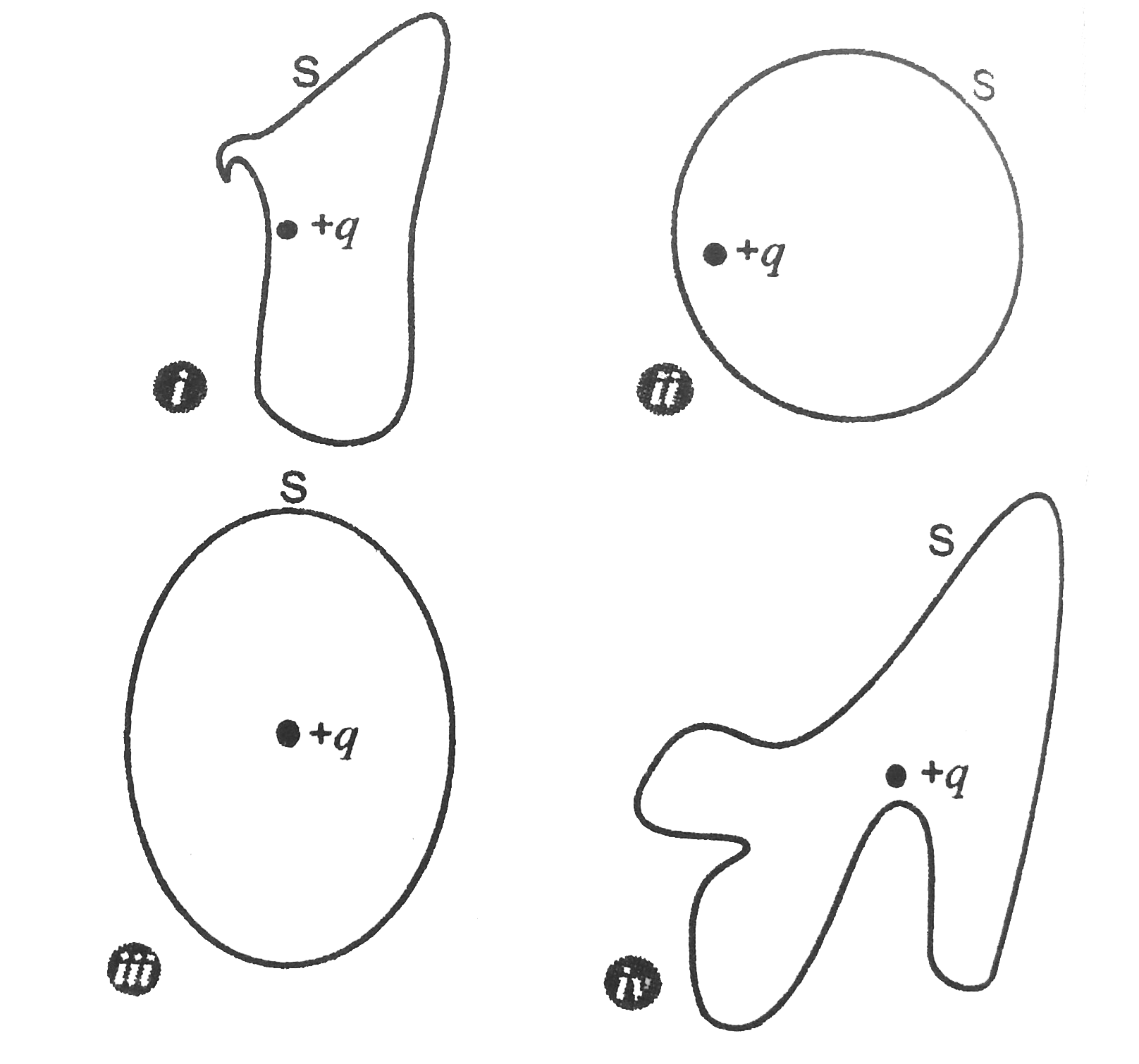
View SolutionThe electric flux through the surface
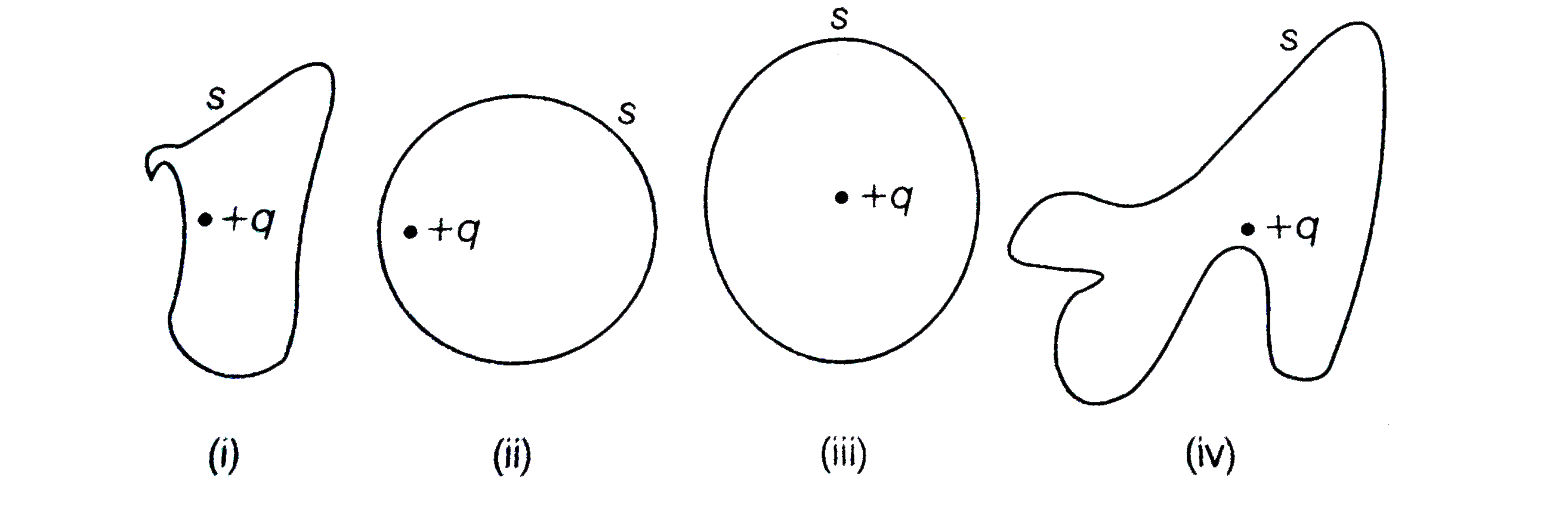
View SolutionIf the electric flux entering and leaving a closed surface are 6×106 and 9×106 SI units respectively, then the net charge inside the surface of permittivity of free space ε0 is
View Solution