A charged spherical conductor of radius R carries a charge Q. a point charge q is placed at an outside point at a distance x from the surface of the sphere. The force experienced by the point charge will be proportional to
1x2
(R+x)2
1(R+x)2
1(R−x)2
The correct Answer is:C
To solve the problem, we need to determine the force experienced by a point charge q placed outside a charged spherical conductor of radius R that carries a charge Q. The point charge is located at a distance x from the surface of the sphere.
1. Identify the Total Distance:
The distance from the center of the spherical conductor to the point charge q is given by the sum of the radius of the sphere R and the distance x from the surface of the sphere to the point charge. Therefore, the total distance d from the center of the sphere to the point charge is:
d=R+x
Hint: Remember that the total distance includes both the radius of the sphere and the distance from the surface to the point charge.
2. Understand the Nature of the Force:
The force F experienced by the point charge q due to the charge Q on the spherical conductor can be described by Coulomb's law. According to Coulomb's law, the force between two point charges is inversely proportional to the square of the distance between them:
F∝1d2
Hint: Recall that the force between two charges decreases with the square of the distance between them.
3. Substitute the Total Distance:
Since we have established that d=R+x, we can substitute this into the expression for the force:
F∝1(R+x)2
Hint: Make sure to replace d with the expression you found in the first step.
4. Conclusion:
From the above steps, we conclude that the force experienced by the point charge q is proportional to:
F∝1(R+x)2
Therefore, the correct answer is that the force experienced by the point charge will be proportional to 1(R+x)2.
Final Answer: The correct option is Option 3: 1(R+x)2.
The distance from the center of the spherical conductor to the point charge q is given by the sum of the radius of the sphere R and the distance x from the surface of the sphere to the point charge. Therefore, the total distance d from the center of the sphere to the point charge is:
d=R+x
The force F experienced by the point charge q due to the charge Q on the spherical conductor can be described by Coulomb's law. According to Coulomb's law, the force between two point charges is inversely proportional to the square of the distance between them:
F∝1d2
Since we have established that d=R+x, we can substitute this into the expression for the force:
F∝1(R+x)2
From the above steps, we conclude that the force experienced by the point charge q is proportional to:
F∝1(R+x)2
Topper's Solved these Questions
- ELECTROSTATICSBook:MARVEL PUBLICATIONChapter:ELECTROSTATICSExercise:TEST YOUR GRASP
Explore 20 Videos
- ELECTRONS AND PHOTONS Book:MARVEL PUBLICATIONChapter:ELECTRONS AND PHOTONS Exercise:TEST YOUR GRASP - 17
Explore 15 Videos
- GRAVITATION Book:MARVEL PUBLICATIONChapter:GRAVITATION Exercise:TEST YOUR GRASP -2
Explore 20 Videos
Similar Questions
Figure shows a uniformly charged sphere of radius R and total charge Q. A point charge q is situated outside the sphere at a distance r from centre of sphere. Find out the following :
(i) Force acting on the point charge q due to the sphere.
(ii) Force acting on the sphere due to the point charge.

View SolutionA square of side d, made from a thin insulating plate, is uniformly charged and carries a total charge of Q. A point charge q is placed on the symmetrical normal axis of the square at a distance d/2 from the plate. How large is the force acting on the point charge ?
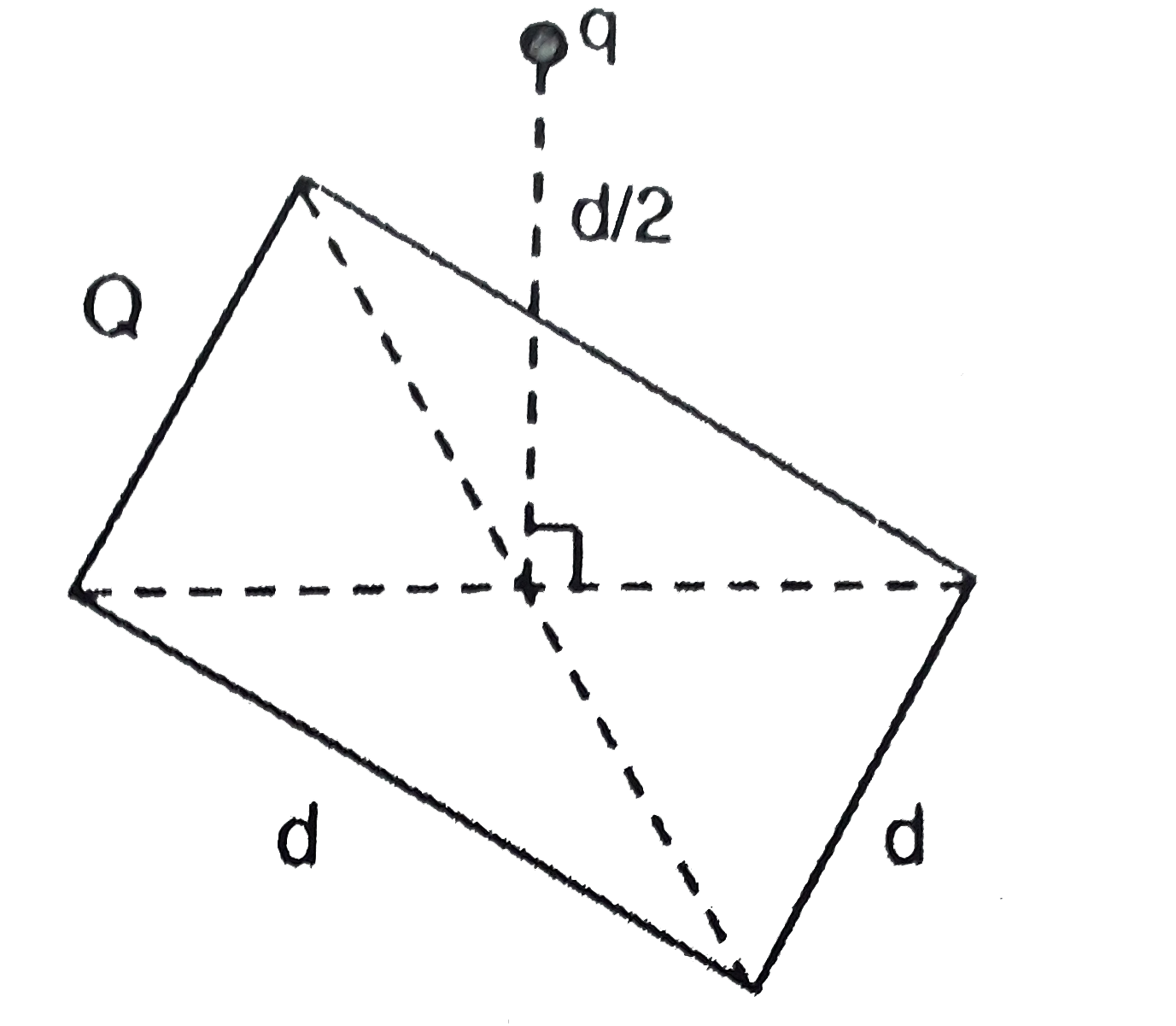
View Solution
Knowledge Check
A conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
A B
B C
C D
D
A thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
A(a) 2Q4πε0RB(b) 2Q4πε0R−2q4πε0RC(c) 2Q4πε0R+q4πε0RD(d) (q+Q)24πε0RThere is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
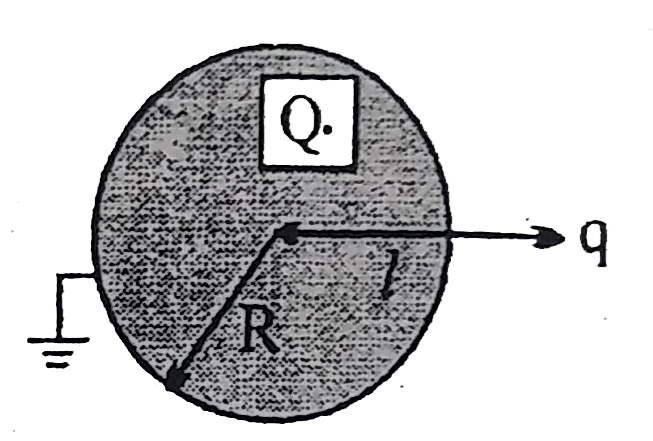
Net charge on the outer surface of conducting sphere isA+QBQ−qR/1C−qR/IDnone
A charge Q is distributed over a line of length L Another point charge q is placed at a distance r from the centre of the line distribution. Then the force experienced by q is
View SolutionA charge Q is distributed over a line of length L Another point charge q is placed at a distance r from the centre of the line distribution.Then the force experienced by q is
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionA conducting spherical shell having inner radius a and outer radius b carries a net charge Q. If a point charge q is placed at the centre of this shell, then the surface charge density on the outer surface of the shell is given as:
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View Solution

