Two spherical bodies A (radius 6cm) and B (radius 18cm) are at temperature T1 and T2 respectively The maximum intensity in the emission spectrum of A is at 500nm and in that of B is at 1500nm considering them to be black bodies, what will be the ratio of the rate of total energy radiated by A to that of B . ?
8
9
10
12
The correct Answer is:B
Using Wien's law, we have
λATA=λBTB ∴TATB=λBλA=1500nm500nm=3
By Stefan's law, rate of radiation of total energy E∝AT4
∴E1E2=4πR2A4πR2B×(TATB)2=(RARB)2×(TATB)2
=(618)2×34=(13)2×34=9
Topper's Solved these Questions
- KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATIONBOOK - MARVEL PUBLICATIONCHAPTER - KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATIONEXERCISE - TEST YOUR GRASP - 9
30 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - MCQ
195 Videos
Similar Questions
Two spherical bodies A (radius 6cm) and B (radius 18cm) are at temperature T1 and T2 respectively The maximum intensity in the emission spectrum of A is at 500nm and in that of B is at 1500nm considering them to be black bodies, what will be the ratio of total energy radiated by A to that of B .
View SolutionConsider two hot bodies B1 and B2 which have temperature 100∘C and 80∘C respectively at t = 0. The temperature of surroundings is 40∘ C. The ratio of the respective rates of cooling R1 and R2 of these two bodies att=0 will be
View Solution
Knowledge Check
Two spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
A(T1T2)2B(T2T1)2C(T1T2)4D(T2T1)4A black body radiates heat at temperatures T1 and T2(T2>T1 the frequency corresponding to maxium energy is
Amore atT1Bmore at T2Cequal for T1 and T2Dindependent of T1 and T2A black body radiates heat at temperatures T1 and T2(T2>T1 the frequency corresponding to maxium energy is
Amore atT1Bmore at T2Cequal for T1 and T2Dindependent of T1 and T2
The plots of intensity versus wavelength for three black bodies at temperatures T1,T2 and T3 respectively are shown in Their temperatures are shown in How their temperatures are related ?
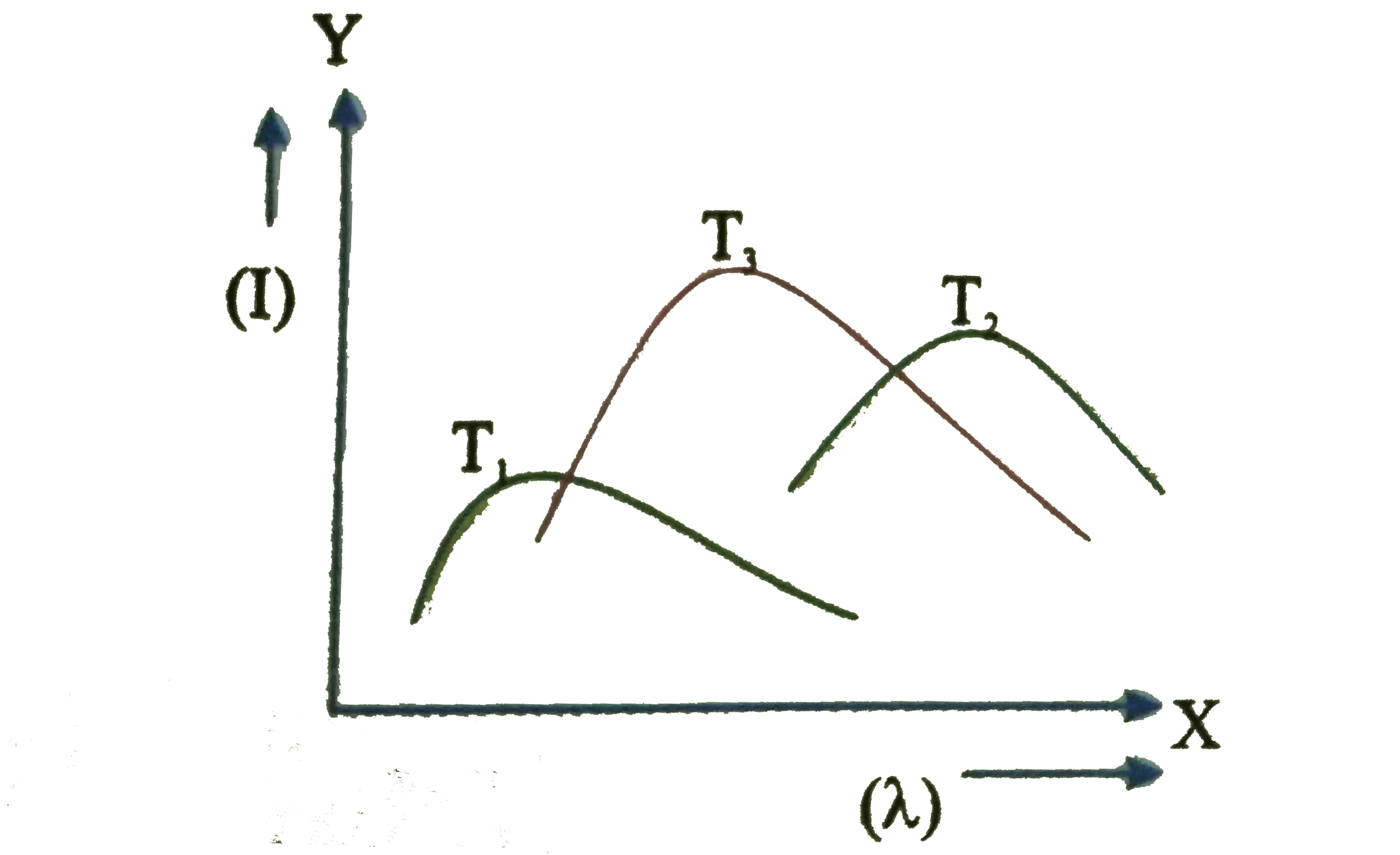 .
.
View SolutionTwo bodies A and B at temperatures T1KandT2K respectively have the same dimensions. Their emissivities are in the ratio of 1:3. If they radiate the same amount of heat per unit area per unit time, then the relation between their temperatures is given by
View SolutionIf the radius of a star is R and it acts as a black body, what would b the temperature of the star, in which the rate of energy production is Q?
View SolutionTwo black bodies A and B have equal surface areas and are maintained at temperatures 27∘C and 177∘C respectively. What will be the ratio of the thermal energy radiated per second by A to that by B?
View SolutionThe plots of intensity versus wavelength for three black bodies at temperature T1,T2andT3 respectively are as shown. Their temperatures are such that
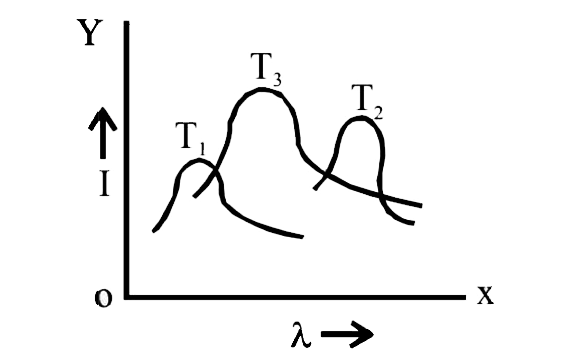
View Solution
