Standing waves are produced on a string of length 2 m and of linear mass density kg/m . What is the frequency of the harmonic as shown in the figure, if the applied tension is 100 N ?
(##MRV_PHY_MCQ_XII_C08_E01_094_Q01.png" width="80%">
25 Hz
50 Hz
Hz
Hz
The correct Answer is:C
The fundamental frequency
Hz
As there are 3 loops on the string , it is vibrating in the third harmonic .
The frequency Hz
Related Playlists
- BOOK - MARVEL PUBLICATIONCHAPTER - STATIONARY WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS (HIGHER LEVEL)75videos
STATIONARY WAVES
- BOOK - MARVEL PUBLICATIONCHAPTER - STATIONARY WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS (STANDARD LEVEL )75videos
STATIONARY WAVES
- BOOK - MARVEL PUBLICATIONCHAPTER - STATIONARY WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS (HIGHER LEVEL )7videos
STATIONARY WAVES
- BOOK - MARVEL PUBLICATIONCHAPTER - SEMICONDUCTORS EXERCISE - MCQs261videos
SEMICONDUCTORS
- BOOK - MARVEL PUBLICATIONCHAPTER - SURFACE TENSION EXERCISE - MULTIPLE CHOICE QUESTIONS . (TEST YOUR GRASP )10videos
SURFACE TENSION
Similar Questions
In the figure shown
(##AHT_PGT_PHY_C10_E01_006_Q01.png" width="80%">View SolutionThe major product of the following reaction is
(##MOD_SPJ_CHE_XII_P2_C12_E07_108_Q01.png" width="80%">View SolutionThe probability distribution of X is
(# #TRG_MAT_MCQ_XII_P2_C08_E02_005_Q01.png" width="80%">
Then P(X is odd)=View SolutionThe p.m.f. of a random variable X is
(# TRG_MAT_MCQ_XII_P2_C08_E02_009_Q 01.png" width="80%">
If b= 2a, thenView SolutionThe displacement of a particle as a function of time is shown in figure. The figure indicates that
(##MOT_CON_NEET_PHY_C23_E02_025_Q01.png" width="80%">View SolutionA cube of 1 m length is under the - pressures given in the figure. Find the magnitude and the direction of the net force on it.
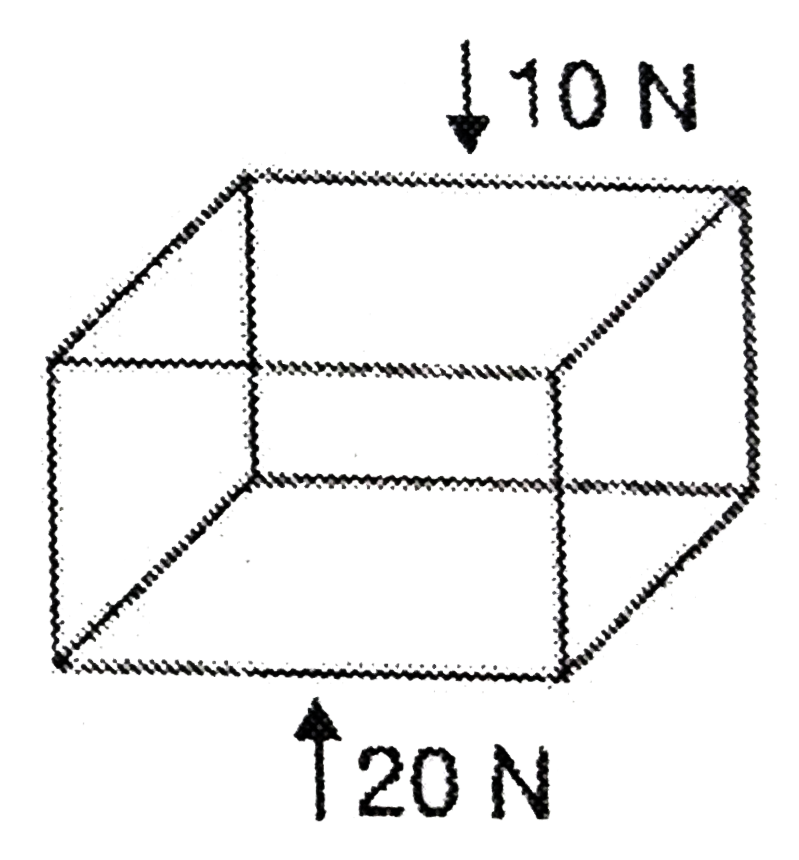 View Solution
View Solution(X) in the reactionCICH2CO2Et+ (##FIITJEE_CHE_MB_08_C04_E03_027_Q01.png" width="80%">
View SolutionFour masses are fixed on a mass less rod as shown in Fig . The moment of inertia about the axis P is about :
(##NAR_NEET_PHY_XI_P2_C05_E06_024_Q01.png" width="80%">View SolutionIn the given figure, a solid sphres is placed on a plank having acceleration a0 (shown in the figure). Then,
(BIT_PHY_C08_E01_047_S01.png" width="80%">View SolutionThree rings each of mass M and radius R are arranged as shown in the figure . The moment of inertia of the system about AB is
(NAR_NEET_PHY_XI_P2_C07_E11_036_Q01.png" width="80%">View Solution

