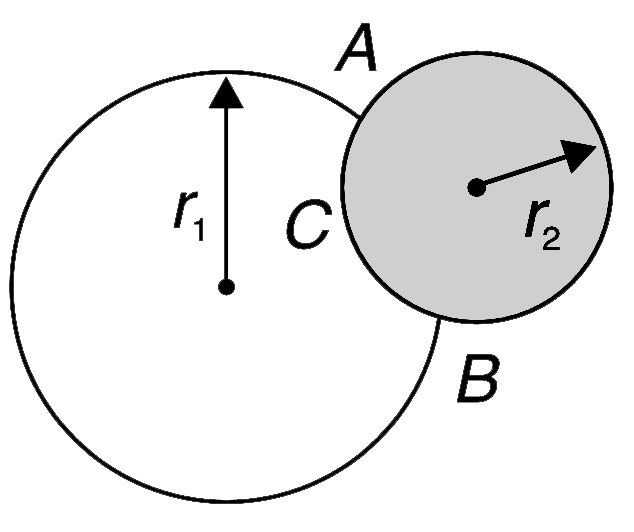
A glass tube of uniform internal radius $(r)$ has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End $1$ has a hemispherical soap bubble of radius $r$ . End $2$ has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.

air form end 1 flows towards end 2, No change in the volume of the soap bubbles

air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases

no change occurs

air from end 2 flows towars end 1 .Volume of the soap bubble at end 1 increases

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

A glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,

A(a) air from end 1 flows towards end 2. No change in the volume of the soap bubbles
B(b) air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases
C(c) no changes occurs
D(d) air from end 2 flows towards end 1. volume of the soap bubble at end 1 increases
Two spherical soap bubbles of radii $r_{1}$ and $r_{2}$ in vacuume collapse under isothermal condition. The resulting bubble has radius $R$ such that
A $R = r_{1} + r_{2}$
B $R = {(r_{1} + r_{2})}_{1}^{\frac{1}{2}}$
C $R = \sqrt{r_{1}^{2} + r_{2}^{2}}$
D $R = [(r_{2} r_{2} (r_{1} + r_{2})]$
Two spherical soap bubbles of a radii 1 cm and 2 cm vacuum coalesce under isothermal conditions . The resultant bubble has a radius of
A $2 / \sqrt{5}$ cm
B $\sqrt{5}$ cm
C $\sqrt{3}$ cm
D $\sqrt{6}$ cm