Water rises in a capillary tube upto a height 'h' so that the upward force due to S.T is balanced by the force due to the weight of the water column. If this force is 90 dyne and surface tension of water is 6×10−2 N/m then the inner circumference of the capillary must be
0.75×10−2 m
1.5×10−2 m
15×10−2 m
0.5×10−2m
The correct Answer is:B
To solve the problem, we need to find the inner circumference of a capillary tube given the upward force due to surface tension and the surface tension of water.
1. Understand the Forces Involved:
The upward force due to surface tension (F) is balanced by the weight of the water column (mg). Therefore, we can write:
F=mg
2. Convert the Given Force:
We are given that the force (F) is 90 dyne. To convert this to Newtons, we use the conversion factor 1 dyne=10−5 N:
F=90 dyne=90×10−5 N=9.0×10−4 N
3. Use the Surface Tension Formula:
The force due to surface tension can also be expressed as:
F=T⋅L
where T is the surface tension and L is the length along which the surface tension acts. In the case of a capillary tube, this length is the inner circumference of the tube, which can be expressed as:
L=2πr
Therefore, we can rewrite the equation as:
F=T⋅(2πr)
4. Substitute Known Values:
We know the surface tension T=6×10−2 N/m and the force F=9.0×10−4 N. Substituting these values into the equation gives:
9.0×10−4=(6×10−2)⋅(2πr)
5. Solve for the Inner Circumference:
Rearranging the equation to solve for 2πr:
2πr=9.0×10−46×10−2
2πr=9.06×10−2 m
2πr=1.5×10−2 m
6. Final Result:
Thus, the inner circumference of the capillary tube is:
2πr=1.5×10−2 m
The upward force due to surface tension (F) is balanced by the weight of the water column (mg). Therefore, we can write:
F=mg
We are given that the force (F) is 90 dyne. To convert this to Newtons, we use the conversion factor 1 dyne=10−5 N:
F=90 dyne=90×10−5 N=9.0×10−4 N
The force due to surface tension can also be expressed as:
F=T⋅L
where T is the surface tension and L is the length along which the surface tension acts. In the case of a capillary tube, this length is the inner circumference of the tube, which can be expressed as:
L=2πr
Therefore, we can rewrite the equation as:
F=T⋅(2πr)
We know the surface tension T=6×10−2 N/m and the force F=9.0×10−4 N. Substituting these values into the equation gives:
9.0×10−4=(6×10−2)⋅(2πr)
Rearranging the equation to solve for 2πr:
2πr=9.0×10−46×10−2
2πr=9.06×10−2 m
2πr=1.5×10−2 m
Thus, the inner circumference of the capillary tube is:
2πr=1.5×10−2 m
Topper's Solved these Questions
- SURFACE TENSION Book:MARVEL PUBLICATIONChapter:SURFACE TENSION Exercise:MULTIPLE CHOICE QUESTIONS . (HIGHER LEVEL)
Explore 35 Videos
- SURFACE TENSION Book:MARVEL PUBLICATIONChapter:SURFACE TENSION Exercise:MULTIPLE CHOICE QUESTIONS . (GRAPHICAL MCQS)
Explore 3 Videos
- SURFACE TENSION Book:MARVEL PUBLICATIONChapter:SURFACE TENSION Exercise:MULTIPLE CHOICE QUESTIONS . (TEST YOUR GRASP )
Explore 10 Videos
- STATIONARY WAVESBook:MARVEL PUBLICATIONChapter:STATIONARY WAVESExercise:TEST YOUR GRASP-8
Explore 20 Videos
- WAVE MOTIONBook:MARVEL PUBLICATIONChapter:WAVE MOTIONExercise:Test your grasp
Explore 15 Videos
Similar Questions
Water rises in a capillary tube upto a certain height such that the upward force of surface tension balances the force of 75×10−5N due to weight of the liquid. If surface tension of water is 6×10−2Nm−1, what must be the internal circumference of the capillary tube?
View SolutionWhen one end of the capillary is dipped in water, the height of water column is 'h'. The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of water column . The inner circumference of the capillary is
(Surface tension of water =7×10−2N/m)
View Solution
Knowledge Check
Water rises in a capillary tube to a certain height such that the upward force due to surface tension is balanced by 75×10−4 newton force due to the weight of the liquid. If the surface tension of water is 6×10^-2 newton/metre the inner circumference of the capillary must be:
A1.25×10−3metreB0.50×10−2metreC6.5×10−2metreD12.5×10−2metreWater rises in a capillary upto a height h. If now this capillary is tilted by an angle of 45∘ then the length of the water column in the capillary becomes-
A2hBh2Ch√2Dh√2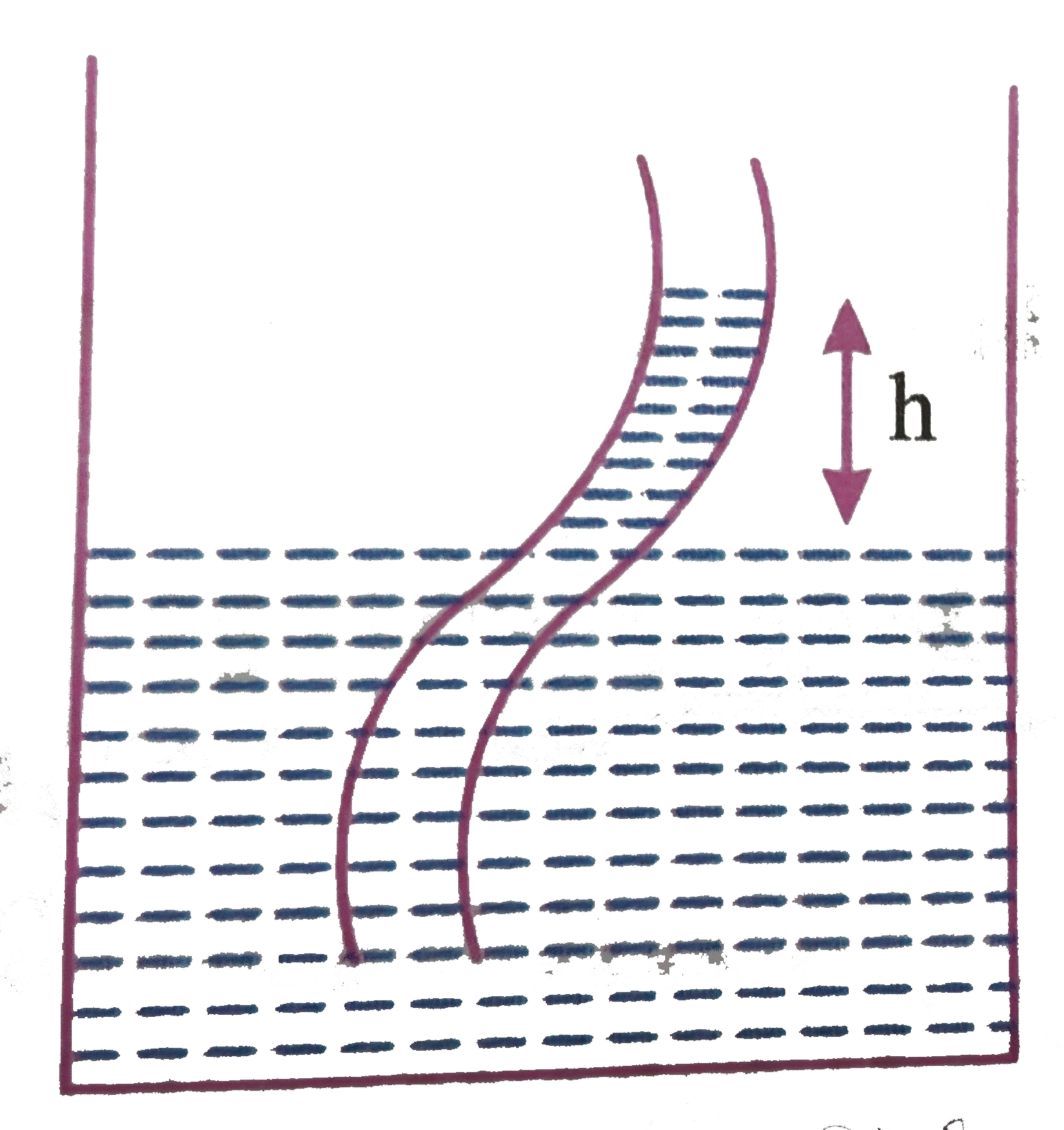
Water rises in a straight capillary tube upto a height of 5 cm when held vertical in water. If the tube is bent as shown figure then the height of water column in it will beA5 cmBless than than 5cmCmore than 5 cmD5cosα
Water rises in a capillary tube to a height H, when the capillary tube is vertical. If the same capillary is now inclined to the vertical the length of water column in it will
View SolutionIn a capillary tube water rises upto a certain height such that the upward force of surface tension balances the force of 75×10−4N. Due to weight of water, the internal circumference of capillary must be (ST of water=6×10−2N/m)
View SolutionWater rises in a capillary tube of diameter 0.2×102m upto a height of 1.5 cm. The surface tension of water is-
View SolutionWhen a capillary is dipped in water, water rises 0.015 m in it. If the surface tension of water is 75×10−3N/m , the radius of capillary is
View SolutionWater rises to a height h in a capillary at the surface of earth. On the surface of the moon the height of water column in the same capillary will be-
View Solution

