Question

A concave mirrorr of focal length ${\displaystyle f_1}$ is placed at a distance of ${\displaystyle d}$ from a convex lens of focal length ${\displaystyle f_2}$. A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance ${\displaystyle d}$ must equal.

Options

A. `f_(1) +f_(2)`
B. `-f_(1)+f_(2)`
C. `2f_(1)+f_(2)`
D. `-2f_(1)+f_(2)`

Answer

C

Explanation

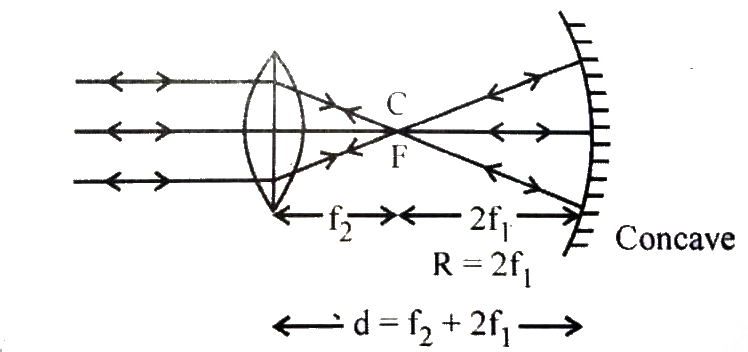
The parallel beam of light is focused at the focus F of the convex lens. If F coincides with the centre of curvature C of the concave mirror, then the rays reflected from the mirror will again come to C and the rays from F, will become parallel after passing through the lens.
`therefore ` Distance `d= f_(2)+R=f_(2)+2f_(1)`