When the surface of a lake is calm , a fish submerged in water will see the entire outside world within an inverted cone whose vertex is situated at the eye of the fish . What is the vertex angle of the cone ?
(anw=43) and sin49∘=0.75
110∘
98∘
48∘
68∘
The correct Answer is:B
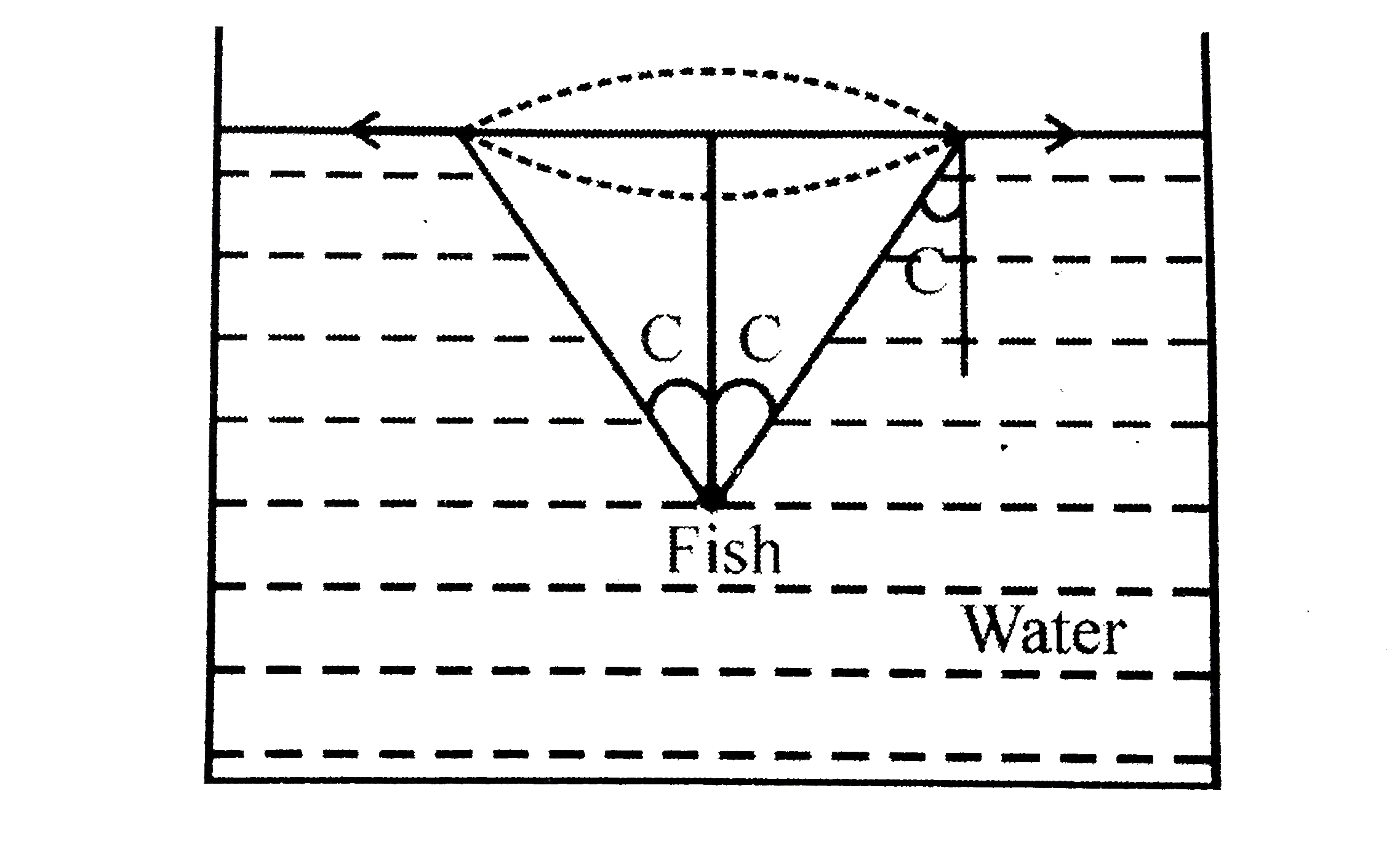
anw=43
If C is the critical angle , then
sinC=1anw=14/3=34=0.75
∴C=sin−1(0.75∘)=90∘
∴ Vertex angle of the cone = 2×49∘=98∘
Topper's Solved these Questions
- REFRACTION OF LIGHT BOOK - MARVEL PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - Test Your Grasp
10 Videos
- RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)BOOK - MARVEL PUBLICATIONCHAPTER - RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)EXERCISE - TEST YOUR GRASP
10 Videos
- VECTORSBOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - TEST YOUR GRASP
10 Videos
Similar Questions
For a fish under water, the entire outside view is confined within a cone. Draw an appropriate ray diagram for this and calculate the value of semi-vertical angle of the cone. Refractive index of water =4/3
View SolutionThe refractive index of water is 4/3. Determine the angle of the cone within which the entire outside view will be confined for a fish under water.
View Solution
Knowledge Check
A fish at a depth of √7 cm bleow the surface of water sees the outside world through a circular horizon. What is the radius of the circular horizon? [aμw=43]
A4 cmB3 cmC√7cmD1 cmAn air masked eye placed inside water refractive index, μ sees the outside world. The vertex angle of the cone in which the eye will see the outside world is
A2sin−1(1/μ)B2cos−1(1/μ)C2sin−1√(μ2−1)D2cos−1√(μ2−1)A fist looking from within water sees the outside world through a circular horizon. If the fish √7 cm below the surface of water, what will be the radius of the circular horizon
A3.0 cmB4.0 cmC4.5 cmD5.0 cm
The refractive index of water is 4/2. Determine the angle of the cone within which the entire outside view will be confined for a fish under water.
View SolutionA fish situated at a depth h below the surface of water in a lake ,can see the outside objects in air through a circular aperature of radius r . What is the radius of the aperture in terms of h and n ,where n=anw? [anw = R.I. of water w.r.t. air]
View SolutionA fish looking up through the water sees the outside world contained in circular horizon. If the R.I. of water 43 and tne fish is 12 cm below the surface, the radius of this circle in cm is-
View SolutionA fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 4/3 and the fish is 12cm below the surface, the radius of this circle in cm is
View SolutionA fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 43 and the fish is 12 cm below the surface, the radius of this circle is cm is
View Solution
