Question

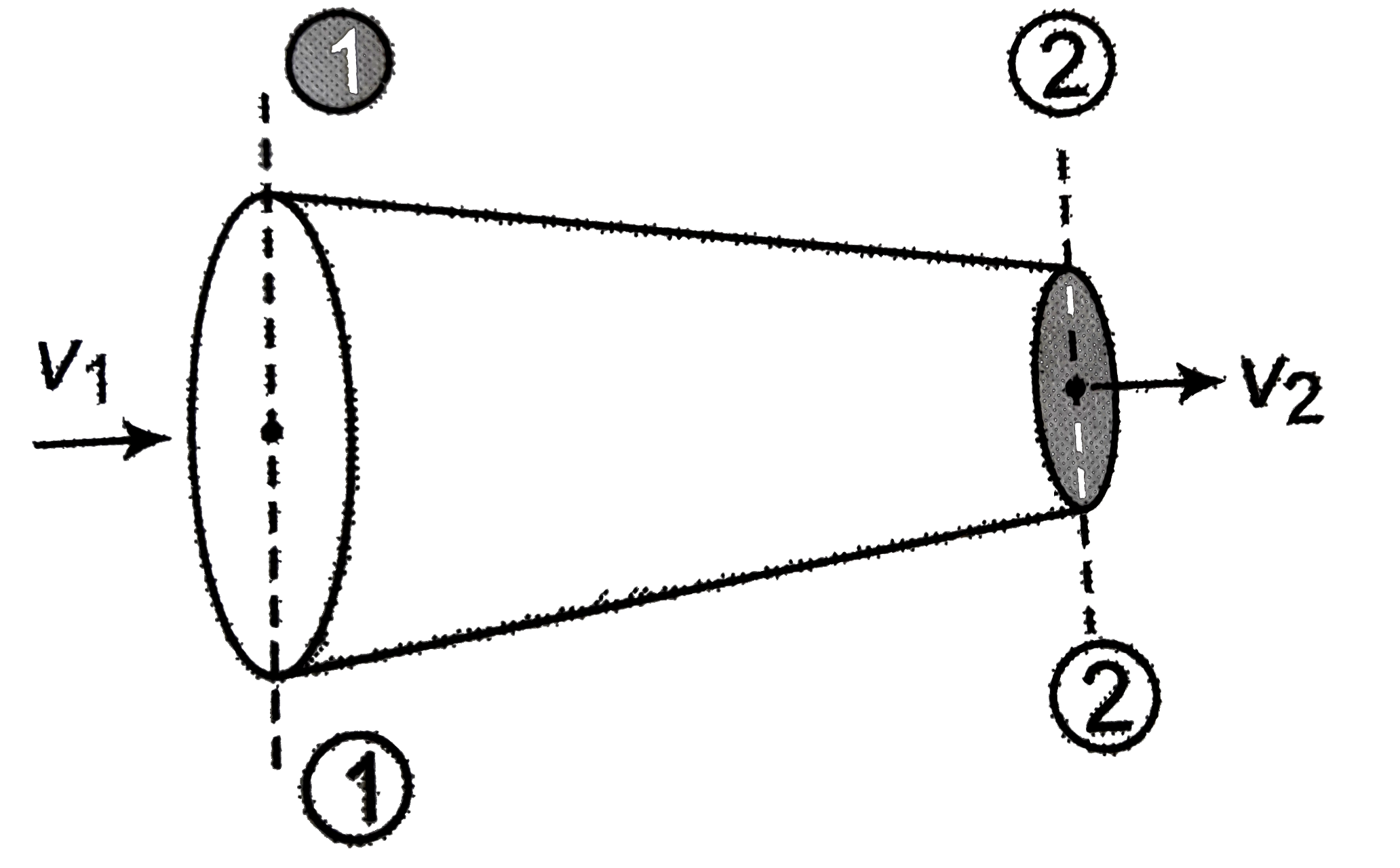
There is a stream line flow of water in a horizontal pipeline ofnon-unifon11 cross-section . The velocities of water at two points. A and B in the pipe are 1 m/s and 2 m/s. The pressure at A is 2000 pascal. What is the pressure at B ?

Options

A. 300 Pa
B. 400 Pa
C. 500 Pa
D. 600 Pa

Answer

C

Explanation

To solve the problem of finding the pressure at point B in a horizontal pipeline with a non-uniform cross-section, we can use Bernoulli's equation, which relates the pressure, velocity, and height of a fluid in steady flow.

1. Understand the Given Data:
- Velocity at point A, \( v_1 = 1 \, \text{m/s} \)
- Velocity at point B, \( v_2 = 2 \, \text{m/s} \)
- Pressure at point A, \( P_1 = 2000 \, \text{Pa} \)
- The flow is horizontal, so the height difference \( h \) is zero.

2. Write Bernoulli's Equation:
Since the flow is horizontal, we can ignore the potential energy term (height). Bernoulli's equation simplifies to:
\( P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2} \rho v_2^2 \)
Where \( \rho \) is the density of water, which is approximately \( 1000 \, \text{kg/m}^3 \).

3. Rearrange the Equation to Solve for \( P_2 \):
\( P_2 = P_1 + \frac{1}{2} \rho v_1^2 - \frac{1}{2} \rho v_2^2 \)

4. Substitute the Known Values:
- Substitute \( P_1 = 2000 \, \text{Pa} \)
- Substitute \( \rho = 1000 \, \text{kg/m}^3 \)
- Substitute \( v_1 = 1 \, \text{m/s} \) and \( v_2 = 2 \, \text{m/s} \)

\( P_2 = 2000 + \frac{1}{2} \times 1000 \times (1^2) - \frac{1}{2} \times 1000 \times (2^2) \)

5. Calculate the Terms:
- Calculate \( \frac{1}{2} \times 1000 \times (1^2) = 500 \)
- Calculate \( \frac{1}{2} \times 1000 \times (2^2) = 2000 \)

Now substitute these values back into the equation:
\( P_2 = 2000 + 500 - 2000 \)

6. Final Calculation:
\( P_2 = 2000 + 500 - 2000 = 500 \, \text{Pa} \)

Conclusion:
The pressure at point B, \( P_2 \), is \( 500 \, \text{Pa} \).

---