In a streamline flow if the gravitational head is h, then the kinetic and pressure heads are
1/2v2/g and p/ρ
1/2v2/g and p/ρg
1/2v and p/ρ
1/2v and p/ρg
The correct Answer is:A
To solve the problem, we need to determine the kinetic and pressure heads in a streamline flow when the gravitational head is given as h. We will use Bernoulli's equation, which relates the pressure, kinetic energy, and gravitational potential energy in a fluid flow.
1. Understanding Bernoulli's Equation:
The Bernoulli equation for a streamline flow can be expressed as:
P+12ρV2+ρgh=constant
where:
- P is the pressure,
- ρ is the fluid density,
- V is the flow velocity,
- g is the acceleration due to gravity,
- h is the height or gravitational head.
2. Identifying the Heads:
In the context of the problem:
- The gravitational head is represented by h.
- The kinetic head is given by V22g.
- The pressure head is given by Pρg.
3. Expressing the Total Head:
According to Bernoulli's principle, the sum of the pressure head, kinetic head, and gravitational head is constant along a streamline. Therefore, we can express the total head as:
H=Pρg+V22g+h
where H is the total head.
4. Finding Kinetic and Pressure Heads:
Since the gravitational head h is given, we can rearrange the equation to isolate the kinetic and pressure heads:
- Kinetic Head:
Kinetic Head=V22g
- Pressure Head:
Pressure Head=Pρg
5. Conclusion:
In a streamline flow with a gravitational head h, the kinetic head and pressure head can be calculated using the above formulas. The total head remains constant, and the values of kinetic and pressure heads will depend on the flow velocity V and the pressure P.
Final Result:
- Kinetic Head: V22g
- Pressure Head: Pρg
The Bernoulli equation for a streamline flow can be expressed as:
P+12ρV2+ρgh=constant
where:
- P is the pressure,
- ρ is the fluid density,
- V is the flow velocity,
- g is the acceleration due to gravity,
- h is the height or gravitational head.
In the context of the problem:
- The gravitational head is represented by h.
- The kinetic head is given by V22g.
- The pressure head is given by Pρg.
According to Bernoulli's principle, the sum of the pressure head, kinetic head, and gravitational head is constant along a streamline. Therefore, we can express the total head as:
H=Pρg+V22g+h
where H is the total head.
Since the gravitational head h is given, we can rearrange the equation to isolate the kinetic and pressure heads:
- Kinetic Head:
Kinetic Head=V22g
- Pressure Head:
Pressure Head=Pρg
In a streamline flow with a gravitational head h, the kinetic head and pressure head can be calculated using the above formulas. The total head remains constant, and the values of kinetic and pressure heads will depend on the flow velocity V and the pressure P.
- Kinetic Head: V22g
- Pressure Head: Pρg
Topper's Solved these Questions
- FRICTIONAL IN SOLIDS AND LIQUIDS BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP
10 Videos
- FORCE, WORK AND TORQUEBOOK - MARVEL PUBLICATIONCHAPTER - FORCE, WORK AND TORQUEEXERCISE - TEST YOUR GRASP
10 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - TEST YOUR GRASP
10 Videos
Similar Questions
Knowledge Check
Streamline flow is more likely for liquid with
Ahigh density and high viscosityBlow density and low viscosityChigh density and low viscosityDlow density and high viscosityHead in the clouds
ATo daydreamBTo be very tallCTo be very lazyDTo feel giddyWater is flowing in streamline motion in the tube shown in fig. pressure is
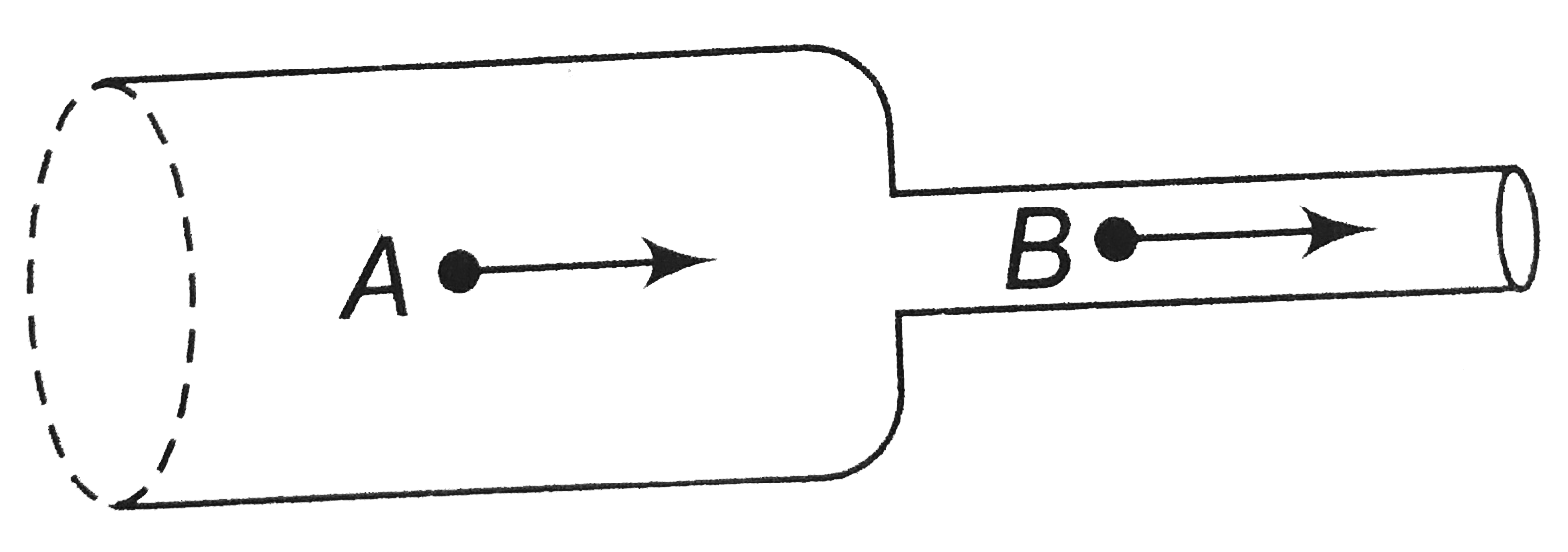 Amore at A then that at BBequal to A and at BClesser at A then that at BDnormal at A and B
Amore at A then that at BBequal to A and at BClesser at A then that at BDnormal at A and B
Expalin streamline flow, laminar flow and turbulent flow.
View SolutionWater flows in a streamline manner through a cappilary tube of radius a. The pressure difference being P and the rate of flow is Q . If the radius is reduced to a/2 and the pressure difference is increased to 2P, then find the rate of flow.
View SolutionWhat is pressure head and velocity head?
View SolutionFor the streamline flow of an ideal fluid flowing horizontally, the pressure___where velocity increases.
View SolutionWhen a capillary tube is connected to a pressure head quantity of water flows per secind is V (in c.c.) if another tube of same length but half the radius is connected to the first in series to the same pressure head, the quantity of water flowing through them per sencond will be (in c.c)
View Solution
