If ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =
4 ¯¯¯¯¯¯AC
3 ¯¯¯¯¯¯AC
2 ¯¯¯¯¯¯CA
¯¯¯¯¯¯AC
The correct Answer is:C
To solve the problem, we need to evaluate the expression ¯AB+2¯BC+3¯CD+4¯DA for a square ABCD.
1. Identify the Vectors:
- Let the length of each side of the square be a.
- The vectors can be represented as:
- ¯AB=a^i (assuming A is at the origin and B is to the right)
- ¯BC=a^j (B to C is upwards)
- ¯CD=−a^i (C to D is to the left)
- ¯DA=−a^j (D to A is downwards)
2. Substituting the Vectors into the Expression:
- Substitute the vectors into the expression:
¯AB+2¯BC+3¯CD+4¯DA=a^i+2(a^j)+3(−a^i)+4(−a^j)
3. Simplifying the Expression:
- Combine the terms:
=a^i+2a^j−3a^i−4a^j
- Group the ^i and ^j components:
=(a−3a)^i+(2a−4a)^j
=−2a^i−2a^j
4. Factoring Out Common Terms:
- Factor out −2a:
=−2a(^i+^j)
5. Final Result:
- The final result can be expressed as:
=−2a(^i+^j)
Conclusion:
The expression ¯AB+2¯BC+3¯CD+4¯DA simplifies to −2a(^i+^j).
- Let the length of each side of the square be a.
- The vectors can be represented as:
- ¯AB=a^i (assuming A is at the origin and B is to the right)
- ¯BC=a^j (B to C is upwards)
- ¯CD=−a^i (C to D is to the left)
- ¯DA=−a^j (D to A is downwards)
- Substitute the vectors into the expression:
¯AB+2¯BC+3¯CD+4¯DA=a^i+2(a^j)+3(−a^i)+4(−a^j)
- Combine the terms:
=a^i+2a^j−3a^i−4a^j
- Group the ^i and ^j components:
=(a−3a)^i+(2a−4a)^j
=−2a^i−2a^j
- Factor out −2a:
=−2a(^i+^j)
- The final result can be expressed as:
=−2a(^i+^j)
The expression ¯AB+2¯BC+3¯CD+4¯DA simplifies to −2a(^i+^j).
Topper's Solved these Questions
- VECTORSBook:MARVEL PUBLICATIONChapter:VECTORSExercise:PREVIOUS YEARS MHT-CET EXAM QUESTIONS
Explore 10 Videos
- VECTORSBook:MARVEL PUBLICATIONChapter:VECTORSExercise:TEST YOUR GRASP
Explore 20 Videos
- TRIGONOMETRIC FUNCTIONSBook:MARVEL PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONSExercise:TEST YOUR GRASP: CHAPTER 3-3.3
Explore 13 Videos
Similar Questions
Knowledge Check
If ABCD is a square then,
2¯¯¯¯¯¯AB+4¯¯¯¯¯¯BC+5¯¯¯¯¯¯CD+7¯¯¯¯¯¯DA=A2¯¯¯¯¯¯BDB3¯¯¯¯¯¯CAC5¯¯¯¯¯¯DBD2¯¯¯¯¯¯ACIf ABCDE is a pentagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED=
A¯¯¯¯¯¯ACB2¯¯¯¯¯¯ACC2¯¯¯¯¯¯ADD3¯¯¯¯¯¯ADIf ABCDE is a regular penatagon then :
¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AD+¯¯¯¯¯¯ED+¯¯¯¯¯¯AE=A¯¯¯¯¯¯AC−2¯¯¯¯¯¯DCB3¯¯¯¯¯¯AC−2¯¯¯¯¯¯DCC¯¯¯¯¯¯CA−¯¯¯¯¯¯DCD3¯¯¯¯¯¯AC−¯¯¯¯¯¯DC
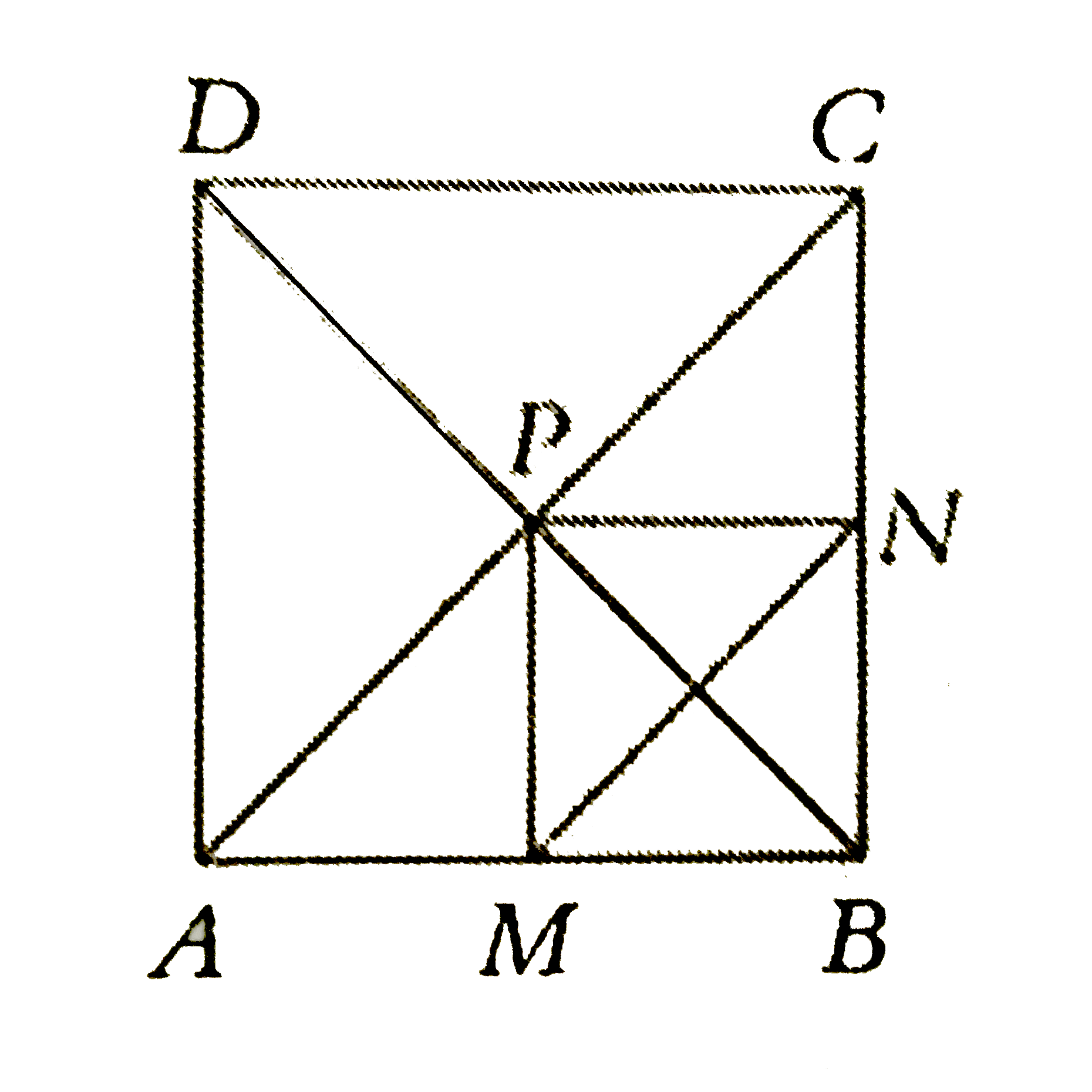
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.
View Solution
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.
View Solution
In the figure above, ABCD is a parallelogram, ¯¯¯¯¯¯BE⊥¯¯¯¯¯¯AB,¯¯¯¯¯¯BG⊥¯¯¯¯¯¯CD, and EBGD is a square. If BG=12 cm and BC=13 cm , then find AB.
View SolutionIf diagonals of a parallelogram ABCD intersect each other in M, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC+¯¯¯¯¯¯OD =
View SolutionΔABC is an isosceles triangle and ¯¯¯¯¯¯AB=¯¯¯¯¯¯AC=2aunit, ¯¯¯¯¯¯BC = a unit. Draw AD⊥BC, and find the length of ¯¯¯¯¯¯AD .
View Solution

