Let , RS be the diameter of the circle x2+y2=1 , where S is the point ( 1,0) . Let P be a variable point (other then R and S ) on the circle and tangents to the circle at s and P meet at the point Q . The normal to the circle at P intersects a line drawn through Q parallel to RS at point E . The locus of E passes through the point (s) Solution in Bengali
(13,1√3)
(14,12)
(13,−1√3)
(14,−12)
The correct Answer is:A, C, D
Step by step video, text & image solution for Let , RS be the diameter of the circle x^(2) + y^(2) = 1 , where S is the point ( 1,0) . Let P be a variable point (other then R and S ) on the circle and tangents to the circle at s and P meet at the point Q . The normal to the circle at P intersects a line drawn through Q parallel to RS at point E . The locus of E passes through the point (s) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE GEOMETRYBook:CHHAYA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:JEE Advanced Archive (2015)
Explore 2 Videos
- CONTINUITY AND DIFFERENTIABILITY Book:CHHAYA PUBLICATIONChapter:CONTINUITY AND DIFFERENTIABILITY Exercise:Sample Questions for Competitive Examination (Assertion - Reason Type)
Explore 2 Videos
- DEFINITE INTEGRAL Book:CHHAYA PUBLICATIONChapter:DEFINITE INTEGRAL Exercise:SAMPLE QUESTIONS FOR COMPETITIVE EXAMINATION ( ASSERTION-REASON TYPE )
Explore 2 Videos
Similar Questions
Let the curve C be the mirror image of the parabola y2=4x with respect to the line x + y + 4 = 0 If A and B are the points of intersection of C with the line y = - 5 , then the distance between A and B is
View SolutionLet f:R→R be a continuous function defined defined by f(x)=1ex+2e−x
Statement−I:f(c)=(1)/(3)"for some "c inRR<br>Statement−II0ltf(x)le(1)/(2sqrt(2))" for all "x in RR
View SolutionStatement-I: ∫π20sinnxdx=∫π20cosnxdx,n∈N
Statement-II: ∫a0f(x)dx=∫a0f(a−x)dx
View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View SolutionP तथा Q वृत्त पर दो बिंदु स्तिथ है तथा केंद्र O है। वृत्त की लघु चाप पर बिंदु R स्तिथ है। बिंदु P तथा Q पर खींची गई स्पर्श रेखाएं बिंदु S पर मिलती है। यदि ∠PSQ=20∘ है, तब ∠PRQ=?
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
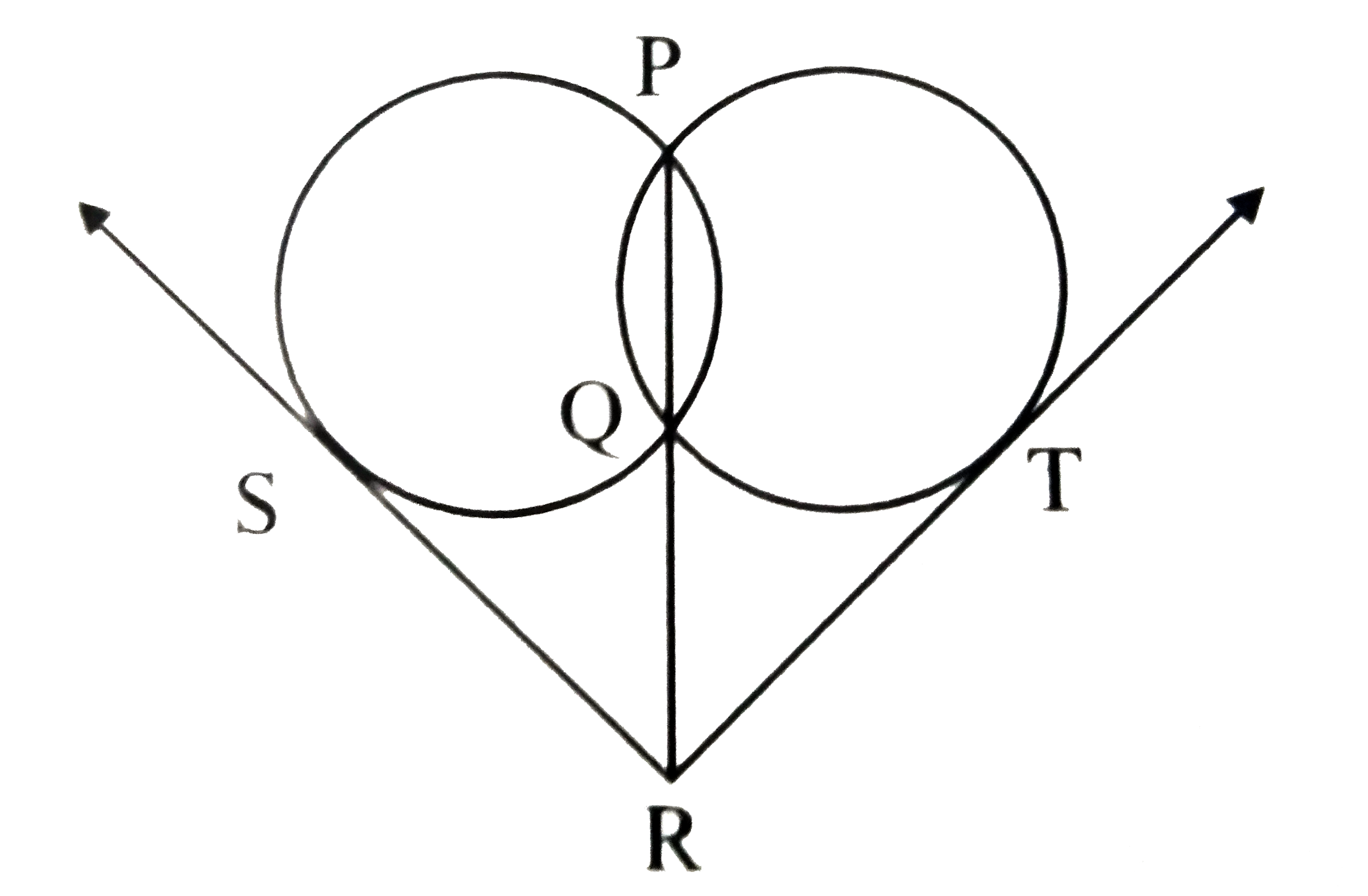
View SolutionA tangent at a point on the circle x2+y2=a2 intersects a concentrie circle S at P and Q. The tangents to S at P and Q meet on the circle x2+y2=b2. The equation to the circle S in
View SolutionA line through the origin meets the circle x2+y2=a2 at P and the hyperbola x2−y2=a2 at. Q the locus of the point of intersection of the tangents at P to the circle and with the tangents at Q to the hyperbola is
View SolutionLet Q(x1,y1) be a variable point and R(1,0) be a point on the circle x2+y2=1andP be the mid -point of QR. Then, the locus of the point P is
View Solutionमाना की RS व्रत x2+y2=1 का व्यास (diameter) है , जहां की S बिंदु (1, 0) है। माना की P (R और S से भिन्न) व्रत पर एक चर (variable) बिंदु है और व्रत पर बिंदुओं S और P पर खींची गई स्पर्शरेखाएं (tangents) बिंदु Q पर मिलती है व्रत के बिंदु P पर अभिलम्ब (normal) उस रेखा को, जो Q से गुजरती है तथा RS के समांतर (parallel) है बिंदु E पर प्रतिच्छेदित करता है तब E का बिन्दुपथ (locus) निम्न बिंदु(ओ) से गुजरता है
View Solutionধরো , x2+y2=1 বৃত্তের একটি ব্যাস RS, যেখানে S বিন্দুটির স্থানাঙ্ক (1, 0)। ধরো , P একটি চলমান বিন্দু (R এবং S ছাড়া) যা বৃওটির ওপর অবস্থিত এবং S , P বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করে। P বিন্দুতে অঙ্কিত বৃত্তটির অভিলম্ব, Q বিন্দুতে অঙ্কিত RS-এর সমান্তরাল সরলরেখাকে E বিন্দুতে ছেদ করে। E-এর সঞ্চারপথ যে বিন্দু/বিন্দুগুলি দিয়ে যায় তা হল—
View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View Solutionमाना की RS व्रत x2+y2=1 का व्यास (diameter) है , जहां की S बिंदु (1, 0) है। माना की P (R और S से भिन्न) व्रत पर एक चर (variable) बिंदु है और व्रत पर बिंदुओं S और P पर खींची गई स्पर्शरेखाएं (tangents) बिंदु Q पर मिलती है व्रत के बिंदु P पर अभिलम्ब (normal) उस रेखा को, जो Q से गुजरती है तथा RS के समांतर (parallel) है बिंदु E पर प्रतिच्छेदित करता है तब E का बिन्दुपथ (locus) निम्न बिंदु(ओ) से गुजरता है
View Solution

