A particle starts from the origin and moves along a straight line. If the velocity of the particle at time t seconds be 10t cm/s, find the distance traversed during first 4 seconds after the start.Solution in Bengali
The correct Answer is:80 cm
Step by step video, text & image solution for A particle starts from the origin and moves along a straight line. If the velocity of the particle at time t seconds be 10t cm/s, find the distance traversed during first 4 seconds after the start. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE BOOK - CHHAYA PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE EXERCISE - MULTIPLE CORRECT ANSWERS TYPE
5 Videos
- DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE BOOK - CHHAYA PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE EXERCISE - B INTEGER ANSWER TYPE
5 Videos
- DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE BOOK - CHHAYA PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE EXERCISE - PART -D
11 Videos
- DETERMINANT BOOK - CHHAYA PUBLICATIONCHAPTER - DETERMINANT EXERCISE - Sample Questions for Competitive Examination (Assertion -Reason Type )
2 Videos
- DIFFERENTIATIONBOOK - CHHAYA PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - Sample Questions for competitive Exams ( E Assertion-Reason Type )
1 Videos
Similar Questions
Which one of the following functions is/are homogenous?
View SolutionIf dydx−xtan(y−x)=1,y(0)=π2 then the value of sin{y(4)−4}e−8 is
View Solutiondydx=4x−5y+35x+y−2
View SolutionIf A=[1242], then show that |2A|=4|A|.
View SolutionStatement -I : f(x) = sin x then f' (π) = f' (3π)
Statement - (ii) : f(x) = sin x then f (π) = f (3π)
View SolutionA particle starts from the origin and moves along a stright line If the velocity of the particle at time t seconds 10t cm/s then find the distance traversed during fist seconds after the start.
View SolutionThe acceleration of a particle moving along a straight line is (6t^(2)-3t)cm/s^(2), at time t seconds,If the velocity of the particle at time 2 seconds be 10cm/s ,find its veloctiy at time t seconds.
View SolutionThe acceleration after t seconds of a particle which starts from rest and moves in a straight line is (8−t5)cms2. Find the velocity of the particle when the acceleration is zero.
View SolutionThe velocity-time graph of a particle in straight line motion is veloity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin. . The distance of the particle from the origin after 8 s is .
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
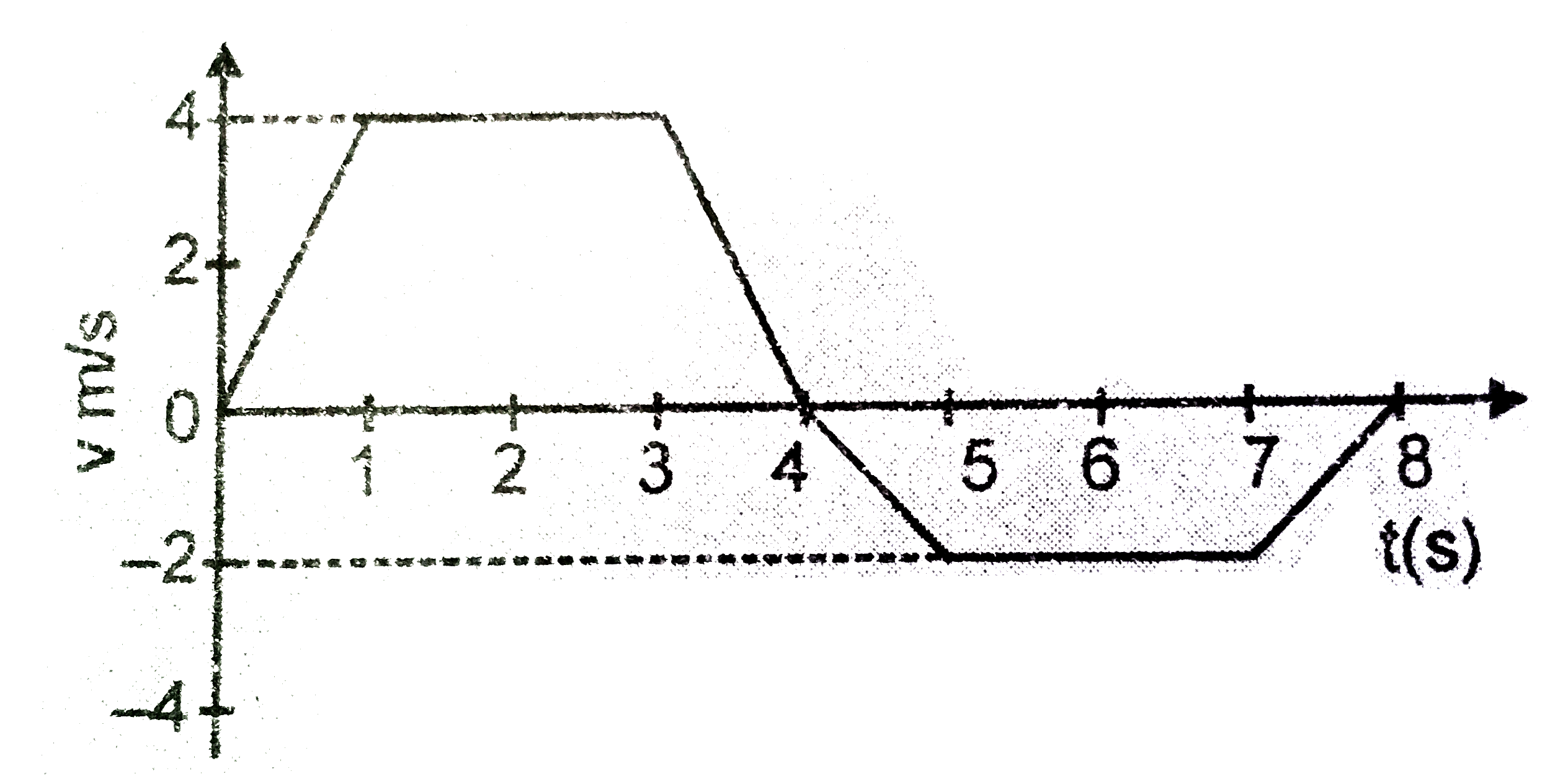
View SolutionA particle starts from the origin with a velocity 5 cm/s and moves in a straight line its accelration at time t seconds being (3t2−5t)cm/s2. Find the velocity of the particle and its distance from the origin at the end of 4 seconds.
View SolutionThe acceleration of a particle moving along a straight line is (6t2−3t)cm/s2, at time t seconds. If the velocity of the particel at time 2 seconds be 10cm/s, find its velocity at time t seconds.
View SolutionA particle starts from rest and moves along a straight line with uniform acceleration. The ratio of distance travelled by the particle during the first three seconds to the distance travelled by the particle during the next three seconds is 3 о 2
View SolutionA particle moves in a straight line and its velocity v at time t seconds is given by v=(6t2−2t+3) cm/sec. Find the distance travelled by the particle during the first 5 second after the start.
View SolutionA particle starts from rest and moves along a straight line with uniform acceleration. The ratio of distance travelled by the particle during the first three seconds to the distance travelled by the particle during the next three seconds is 3 о 2
View Solution
