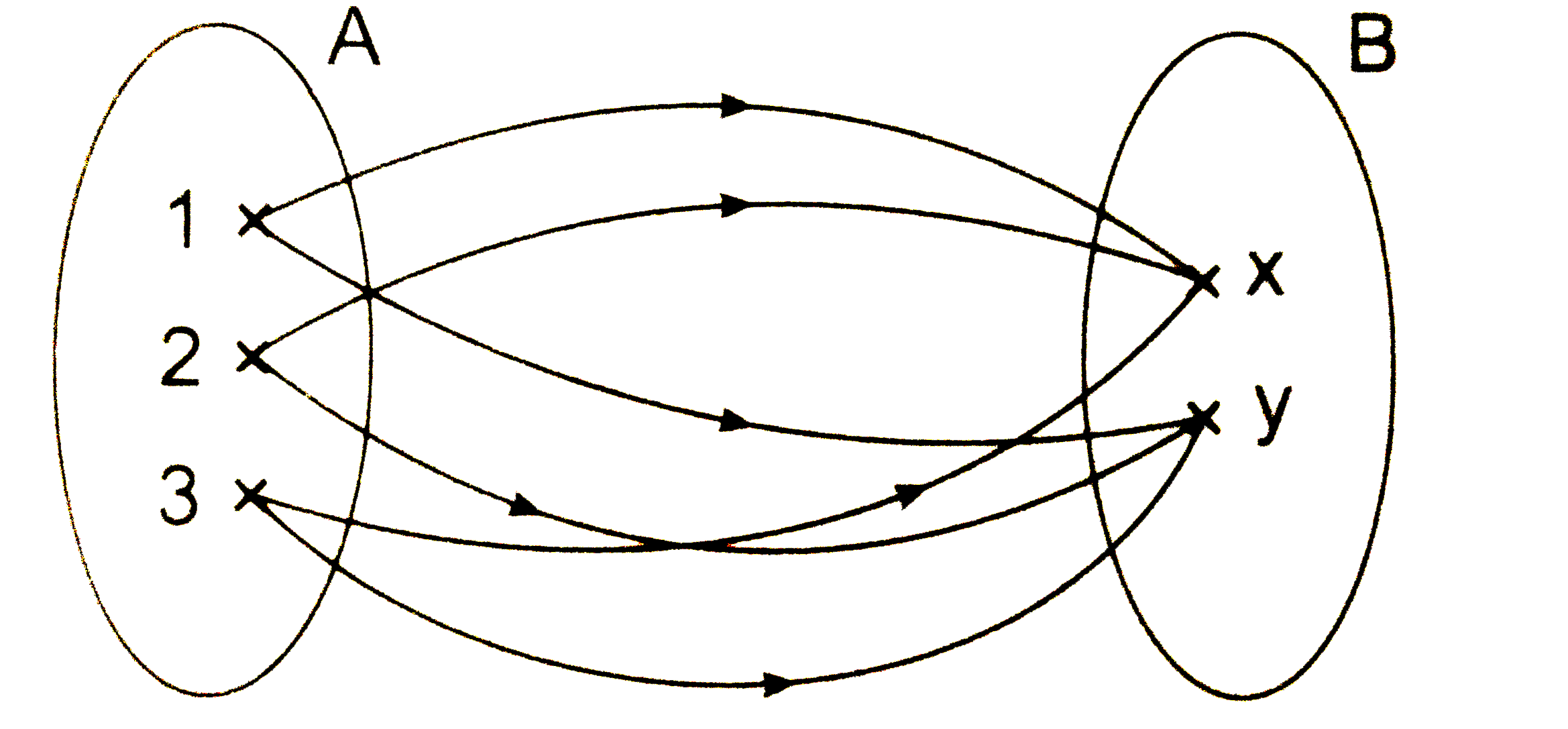
यदि A = {1, 2, 3} और B = {x, y}, तो A×B को तीर आरेख द्वारा निरूपित कीजिए ।
A×B = {(1, x), (1, y), (2, x), (2, y), (3, x), (3, y)}
इनका तीर आरेख निम्नलिखित है -
प्रमेय -यदि A, B और C कोई तीन समुच्चय है, तो
1.A×(B∪C)=(A×B)∪(A×C)
2. A×(B∩C)=(A×B)∩(A×C)
3. A×(B−C)=(A×B)−(A×C)
उपपत्ति -1. माना (x,y)∈A×(B∪C)
⇒x∈A और y∈B∪C
⇒x∈A और (y∈B या y∈C)
⇒(x∈A और y∈B) या (x∈A और y∈C)
⇒(x,y)∈A×B या (x,y)∈A×C
⇒(x,y)∈(A×B)∪(A×C)
∴A×(B∪C)⊆(A×B)∪(A×C)...(1)
पुनः माना (x,y)∈(A×B)∪(A×C)
⇒(x,y)∈A×B या (x,y)∈A×C
⇒(x∈A और y∈B) या (x∈A और y∈C)
⇒x∈A और (y∈B या y∈C)
⇒x∈A और y∈B∪C
⇒(x,y)∈A×(B∪C)
∴(A×B)∪(A×C)⊆A×(B∪C)...(2)
समीकरण (1) और (2) से
A×(B∪C)=(A×B)∪(A×C)
2. माना (x,y)∈A×(B∩C)
⇒x∈A और y∈(B∩C)
⇒x∈A और (y∈B तथा y∈C)
⇒(x∈A और y∈B) तथा (x∈A और y∈C)
⇒(x,y)∈A×B तथा (x,y)∈A×C
⇒(x,y)∈(A×B)∩(A×C)
∴A×(B∩C)⊆(A×B)∩(A×C)...(1)
पुनः माना (x,y)∈(A×B)∩(A×C)
⇒(x,y)∈A×B तथा (x,y)∈(A×C)
⇒(x∈A और y∈B) तथा (x∈A और y∈C)
⇒x∈A और (y∈B तथा y∈C)
⇒x∈A और y∈(B∩C)
⇒(x,y)∈A×(B∩C)
∴(A×B)∩(A×C)⊆A×(B∩C)...(2)
समीकरण (1) और (2) से
A×(B∩C)=(A×B)∩(A×C)
3. माना (x,y)∈A×(B−C)
⇒x∈A और y∈(B−C)
⇒x∈A और (y∈B तथा y∈C)
⇒(x∈A और y∈B) तथा (x∈A और y∈C)
⇒(x,y)∈A×B तथा (x,y)∉A×C
⇒(x,y)∈(A×B)−(A×C)
∴A×(B−C)⊆(A×B)−(A×C)...(1)
पुनः माना (x,y)∈(A×B)−(A×C)
⇒(x,y)∈A×B तथा (x,y)∉A×C
⇒(x∈A और y∈B) तथा (x∈A और y∉C)
⇒x∈A और (y∈B तथा y∉C)
⇒x∈A और y∈(B−C)
⇒(x,y)∈A×(B−C)
∴(A×B)−(A×C)⊆A×(B−C)...(2)
समीकरण (1) और (2) से
A×(B−C)=(A×B)−(A×C)
Topper's Solved these Questions
- सम्बन्ध एवं फलनBook:NOOTAN HINDIChapter:सम्बन्ध एवं फलनExercise:प्रश्नावली 2A
Explore 20 Videos
- सम्बन्ध एवं फलनBook:NOOTAN HINDIChapter:सम्बन्ध एवं फलनExercise:प्रश्नावली 2B
Explore 14 Videos
- समुच्चयBook:NOOTAN HINDIChapter:समुच्चयExercise:विविध प्रश्नावली
Explore 16 Videos
- सम्मिश्र संख्याएँ एवं द्विघात समीकरण Book:NOOTAN HINDIChapter:सम्मिश्र संख्याएँ एवं द्विघात समीकरण Exercise:प्रश्नावली 5F
Explore 10 Videos
Similar Questions
यदि (x3+1,y−23)=(53,13), तो x और y के मान ज्ञात कीजिए ।
View Solutionयदि A = {a, b, c, d} और B = {w, x, y, z}, तो निम्नलिखित में कौन समुच्चय A से B में सम्बन्ध है, कारण सहित बताइए?
(i) R1 = {(a, w), (a, x), (a, y), (a, z)}
(ii) R2 = {(w, b), (z, c), (y, d)}
(iii) R3 = {(a, y), (b, y), (w, y), (d, y)}
(iv) R4 = {(b, z), (b, y), (c, z), (c, w)}
View Solutionनिम्नलिखित समुच्यों में से कौन किसका उपसमुच्चय है इसका निर्णय कीजिएः
A={x:xεR तथा x2−8x+12=0 को संतुष्ट करने वाली सभी वास्तविक संख्याएं x}
B={2,4,6},C={2,4,6,8,…},D=(6)
View Solutionयदि z−1z+1 एक शुद्ध काल्पनिक संख्या है, तो |z| का मान है-
View Solutionसिद्ध कीजिए कि सरल रेखाएँ x=mz+a,y=nz+b और x=m'z+a',y=n'z+b' एक-दूसरे को काटेंगी यदि (a−a')(n−n')=(b−b')(m−m') हो।
View Solutionयदि A xx B = {a, x), (a, y), (b, x), (b, y)}, तो A और B ज्ञात कीजिए ।
View Solutionयदि ज्यामिति आरेख पर बिन्दु P सम्मिश्र संख्या z=x+iy को निरूपित करता है , तो P का बिन्दुपथ ज्ञात कीजिए जबकि
(a)|z−1|=|z−3| (b)|z−1|=5|z+1| (c)arg(z−3)=π3
View Solutionयदि अक्षों को 45∘ कोण से घुमाया जाए तो वक्र x2+y2=a2 का नया समीकरण ज्ञात कीजिए ।
View Solutionयदि →a और→b समान्तर हो , तो →a×→b=……… होगा।
View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि कोणांक (z) = 0
View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि arg(z−2−3i)=π4
View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि ∣∣∣z−2z+2∣∣∣=5
View Solutionयदि [a2+12b0b+3]=[2ab2+4b+102] तो a तथा b के मान ज्ञात कीजिए।
View Solution1 से 5 में अचरों a व b को विलुप्त करते हुए दिये वक्रों के कुल को निरूपित करने वाला अवकल समीकरण ज्ञात कीजिए-
xa+yb=1
View Solutionयदि 1x3−2x2−x+2=Ax−1+Bx+1+Cx−2 हो, तो A+B+C का मान ज्ञात कीजिए।
View Solutionयदि xb+c=yc+a=za+b तो सिद्ध कीजिए कि -
(b−c)x+(c−a)y+(a−b)z=0।
View Solution
